(k−y)2+2x−2y
The correct Answer is:(x−y)(x−y+2)
Step by step video, text & image solution for (k-y)^(2)+2x-2y by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- बीजीय सर्वसमिकाएँBOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - अभ्यास -4.4
16 Videos
- बीजीय सर्वसमिकाएँBOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - अभ्यास -4.5
36 Videos
- बीजीय सर्वसमिकाएँBOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - अभ्यास -4.2
38 Videos
- प्रायिकता या सम्भावितBOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - दीर्घ उत्तरीय प्रश्न
3 Videos
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - वस्तुनिष्ठ प्रश्न
15 Videos
Similar Questions
निम्नलिखित बहुपदो का गुणनखंड निकालें यदि
2x3−3x2−8x−3 का एक गुणनखंड (x+1)है |
View Solutionनिम्नलिखित का गुणनखंड ज्ञात करें :
a3+27b3
View Solutionनिम्नलिखित का गुणनखंड ज्ञात करें।
x2+4x+4
View Solution70 विद्यार्थी के प्राप्ताकों का विवरण नीचे तालिका में दिया गया है।
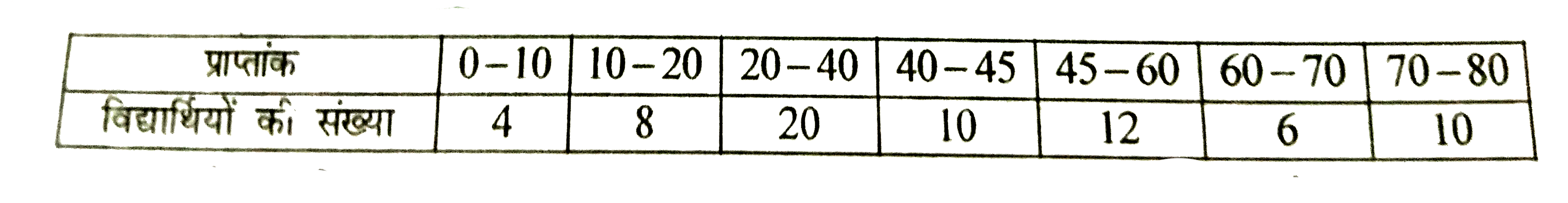
एक विद्यार्थी द्वारा निम्नलिखित वर्ग-अन्तराओं के बीच प्राप्तांकों की प्रायिकता ज्ञात करें।
(i) 0-20 (ii) 0-60
View Solutionएक बिंदु से होकर कितनी रेखाएँ खींची जा सकती हैं ?
View SolutionThe lines 2x−3y=5 and 3x−4y=7 are the diameters of a circle of area 154 sq. units. Then the equation of the circle is x2+y2+2x−2y=62 x2+y2+2x−2y=47 x2+y2−2x+2y=47 x2+y2−2x+2y=62
View SolutionThe solution of the equation (2y-1)dx-(2x+3)dy=0 is (i)(2x-1)/(2y+3)=k( ii) (2y+1)/(2x-3)=k( iii) (2x+3)/(2y-1)=k (iv) (2x-1)/(2y-1)=k
View SolutionThe equation of a hyperbola,conjugate to the hyperbola 2x^(2)+3xy-2y^(2)+3x+y+2=0 is 2x^(2)+3xy-2y^(2)+3x+y+k=0 then k=
View SolutionIf x+y+z=2k then find the value of [(k-2x)^2+(k-2y)^2+(k-2z)^2+5k^2]/(x^2+y^2+z^2)
View Solutionनिम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए -
(x+2y)2+5(x+2y)(2x+y)+6(2x+y)2
View SolutionIf 2x+ky=3,5x−2y=3and3x−y=2 are concurrent then the value of k is -
View SolutionIf 2x+y=0 is one of the lines given by 3x2+kxy+2y2=0, then k=
View SolutionIf the lines x2−y2−2x+2y=0andx+2y+k=0 are concurrent, then k=
View SolutionFind k , if the line y = 2x + k touches the circle x2+y2
−4x−2y=0
View SolutionIf y=2x+k touches x2+y2−4x−2y=0 , then k=
View Solution
