एक समद्विबाहु त्रिभुज ABC जिसमें AB = AC है, की भुजा BC पर दो बिंदु D और E इस प्रकार हैं कि BE = CD है (देखिए चित्र) | दर्शाइए कि AD = AE है |
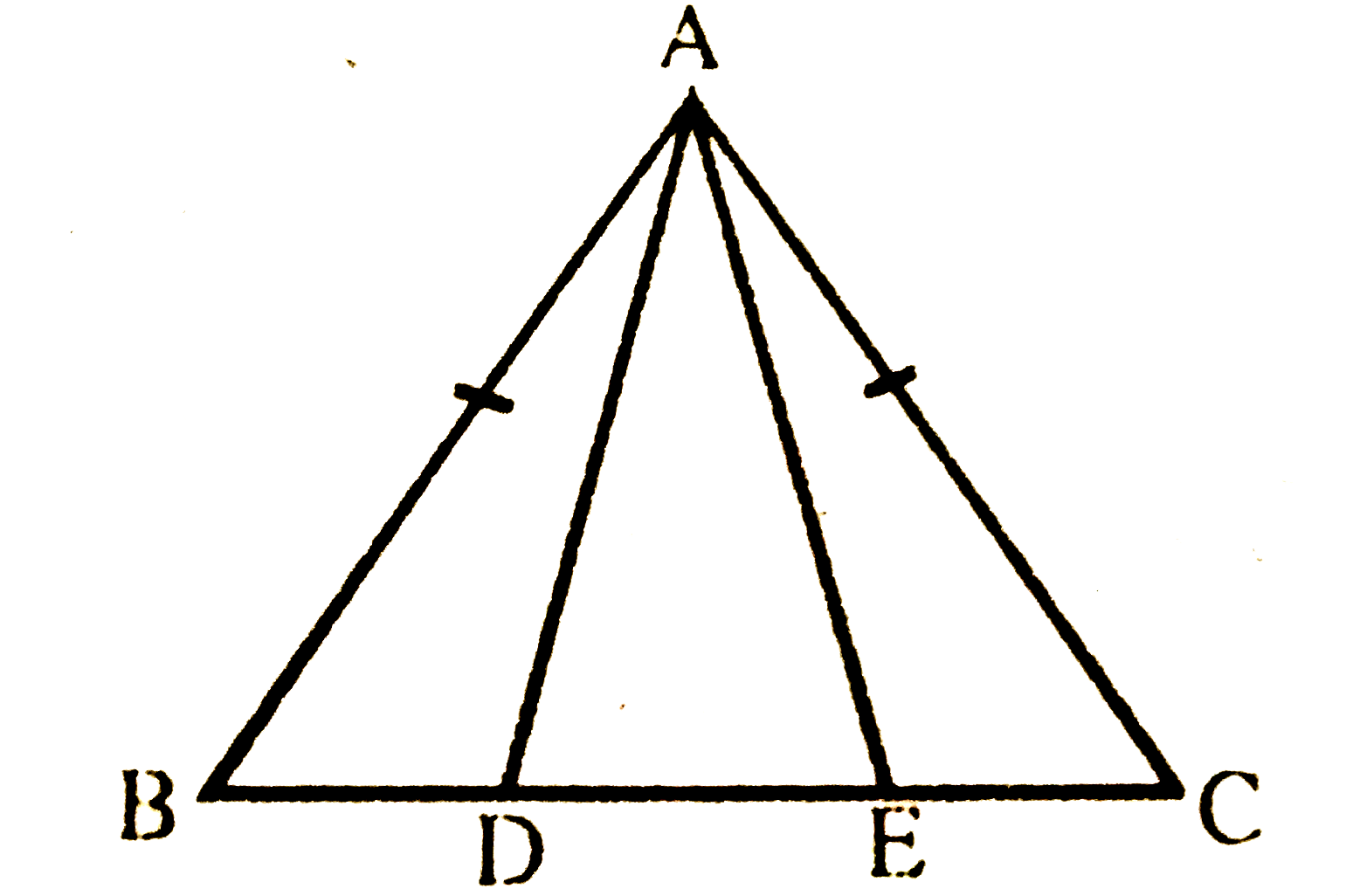
ΔABD और ΔACE में,
AB=AC [दिया है] ...(i)
∠B=∠C [बराबर भुजाओं के सम्मुख कोण] ...(ii)
पुन: BE=CD [दिया है]
इसलिए, BE−DE=CD−DE
अर्थात BD=CE ...(iii)
∴ ΔABD≅ΔACE [(i), (ii), (iii) और SAS नियम से]
अत: AD=AE [CPCT]
Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 (अतिलघु उत्तरीय प्रश्न )
36 Videos
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 लघु उत्तरीय प्रश्न
11 Videos
- ज्यामितीय बनावट ( रचनाएँ ) BOOK - KC SINHACHAPTER - ज्यामितीय बनावट ( रचनाएँ ) EXERCISE - उदाहरण
11 Videos
- दो चरों वाले रैखिक समीकरण BOOK - KC SINHACHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - वस्तुनिष्ट प्रश्न
15 Videos
Similar Questions
यदि किसी त्रिभुज की दो भुजाएँ और उनके .............. कोण, दूसरे त्रिभुज की तदनुरूपी दोनों भुजाओं तथा उनके अंतर्गत कोण के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं |
View Solutionदो त्रिभुजों के सर्वांगसम होने के लिए भुजा-भुजा-भुजा प्रतिबंध को लिखें |
View Solutionएक △ABC बनाये जिसमे BC या (a) =6.6सेमि, CA+AB या (b+c) =10.2 सेमि तथा ∠B=60∘
View Solutionएकघातीय समीकरण ax+by+c=0 के वास्तविक हलो की संख्या है
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn triangle ABC , angle A is a right angle. The lengths of AC and BC 6 cm and 10 cm respectively. Point D is on AB such that BD = 4 cm. What is the length of CD? त्रिभुज ABC में, कोण A समकोण है | AC और BC की लंबाई क्रमशः 6 सेमी और 10 सेमी है | बिंदु D, AB पर इस प्रकार स्थित है कि BD = 4 सेमी है | CD की लंबाई ज्ञात करें |
View SolutionIn triangle ABC , D is a point on side AB, such that, BD = 2cm and DA = 3cm. E is a point on BC such that DE || AC and AC = 4 cm. Then (Area of triangle BDE ): (Area of trapezium ACED) is: त्रिभुज ABC में, D, भुजा AB पर स्थित ऐसा बिंदु है कि BD = 2 सेमी और DA =3 सेमी है | E, BC पर स्थित ऐसा बिंदु है कि DE || AC है और AC =4 सेमी है | तो त्रिभुज (BDE का क्षेत्रफल ) : (समलम्ब ACED का क्षेत्रफल) ज्ञात करें |
View SolutionIn △ABC ,D and E are the points on sides AC and AB, respectively, such that ∠ADE=∠B. If AE = 8 cm, CD = 3 cm, DE= 6 cm and BC = 9 cm, then AD is equal to:
त्रिभुज ABC में, D तथा E क्रमश भुजा AC और AB पर स्थित बिंदु है जो इस प्रकार है कि ∠ADE=∠B है| यदि AE = 8 सेमी, CD = 3 सेमी, DE = 6 सेमी और BC = 9 सेमी है, तो AD का मान किसके बराबर है ?
View Solution
