निम्नांकित प्रश्न के उत्तर दें :
यदि किसी त्रिभुज के शीर्षकोण का अर्द्धक आधार का समद्विभाजन करे तो वह किस प्रकार का त्रिभुज होगा ?
समद्विबाहु त्रिभुज
Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 लघु उत्तरीय प्रश्न
11 Videos
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 दीर्घ उत्तरीय प्रश्न
25 Videos
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - वस्तुनिष्ठ प्रश्न
8 Videos
- ज्यामितीय बनावट ( रचनाएँ ) BOOK - KC SINHACHAPTER - ज्यामितीय बनावट ( रचनाएँ ) EXERCISE - उदाहरण
11 Videos
- दो चरों वाले रैखिक समीकरण BOOK - KC SINHACHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - वस्तुनिष्ट प्रश्न
15 Videos
Similar Questions
दो त्रिभुजों के सर्वांगसम होने के लिए भुजा-भुजा-भुजा प्रतिबंध को लिखें |
View Solutionनीचे की आकृति में AP = AQ और BP = BQ साबित करें कि AB,∠PAQ और ∠PBQ का समद्विभाजक है |
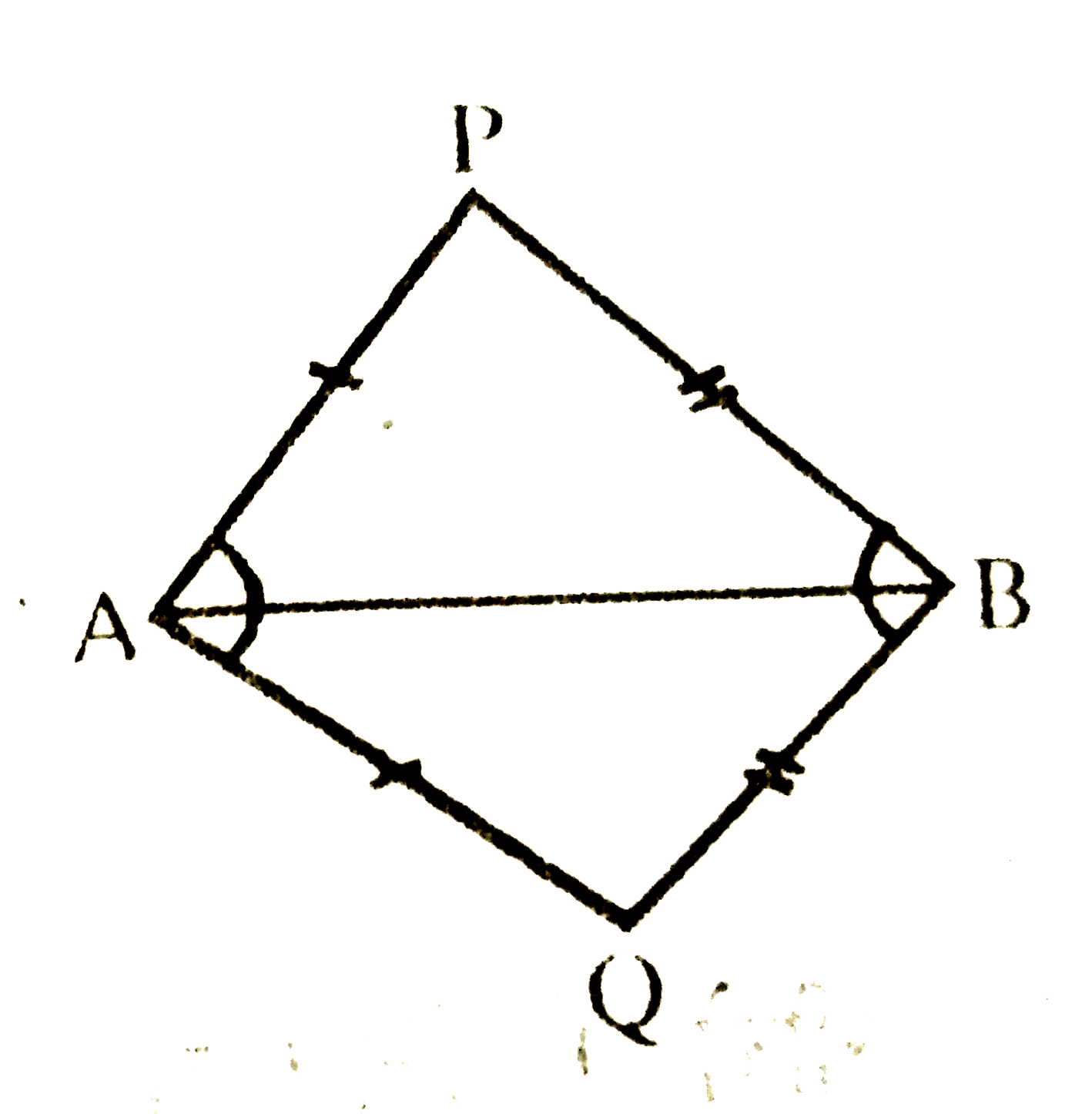
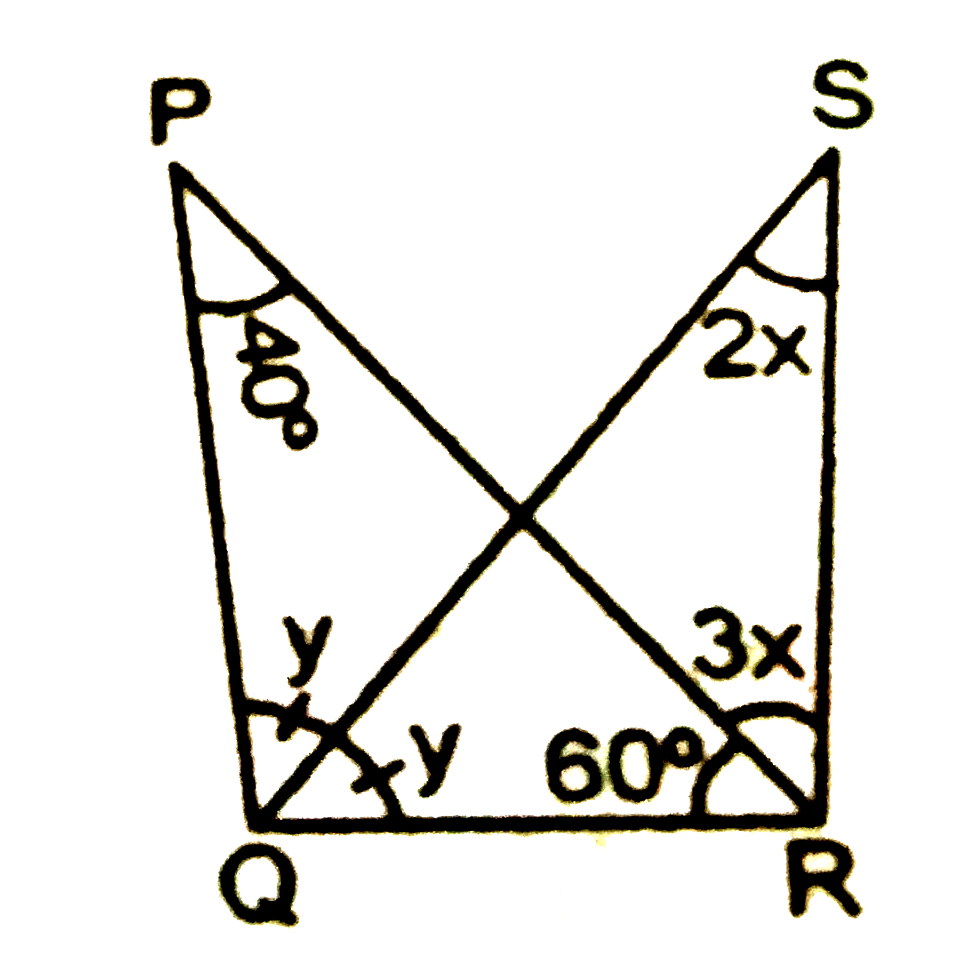
View Solutionनिम्न चित्र में x का मान है:
View Solutionएक △ABC बनाये जिसमे BC या (a) =6.6सेमि, CA+AB या (b+c) =10.2 सेमि तथा ∠B=60∘
View Solutionएकघातीय समीकरण ax+by+c=0 के वास्तविक हलो की संख्या है
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionयदि किसी त्रिभुज के शीर्षो के स्थिति सदिश क्रमश: →a,→b,→c हो तो इस त्रिभुज के केन्द्रक का स्थिति सदिश होगा -
View Solutionसारणिक के अनुप्रयोग | त्रिभुज का क्षेत्रफल | उदाहरण
View Solutionत्रिभुज के अन्तः कोणों का योग गुण
View Solutionहीरोन के सूत्र के प्रयोग से किसी त्रिभुज का क्षेत्रफल ज्ञात करना
View SolutionRevision|त्रिभुज का क्षेत्रफल#!#हीरोन के सूत्र द्वारा#!#महत्वपूर्ण प्रश्न
View SolutionRevision|हीरोन के सूत्र पर आधारित महत्वपूर्ण प्रश्न#!#त्रिभुज का क्षेत्रफल तथा चतुर्भुज का क्षेत्रफल
View Solutionकिसी त्रिभुज का केन्द्रक|कुछ अन्य महत्त्वपूर्ण प्रश्नों के हल
View SolutionRevision |त्रिभुज का क्षेत्रफल #!#बिंदुओं के संरेख होने का प्रतिबंध
View Solutionहीरोन का सूत्र#!#त्रिभुज का क्षेत्रफल#!#परीक्षा के लिए महत्वपूर्ण प्रश्न
View Solutionत्रिभुज |त्रिभुजों के प्रकार |सर्वांगसम आकृतिया |त्रिभुजों का सर्वांगसमता |सारांश
View Solution
