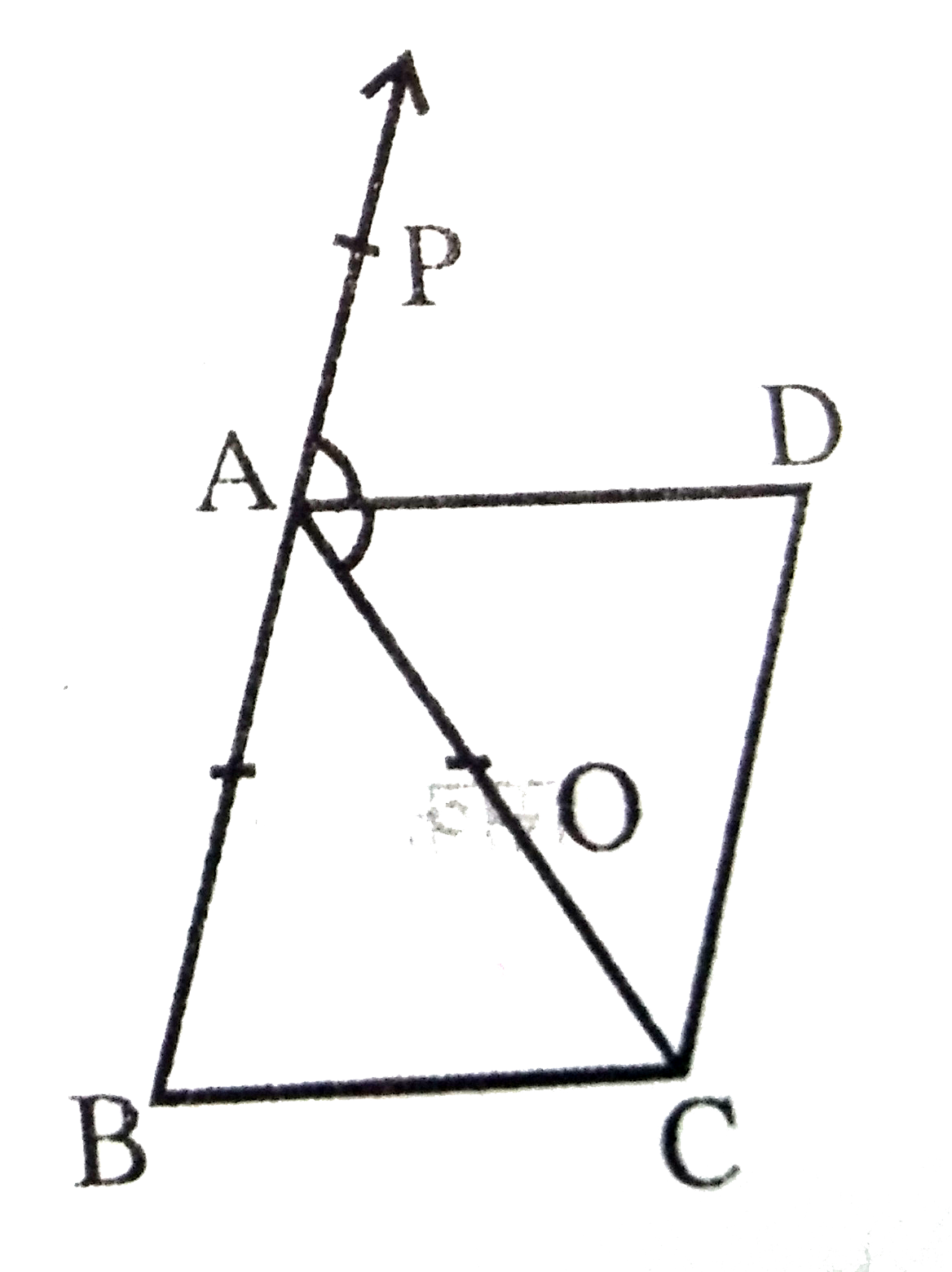
ABC एक समद्विभाहु त्रिभुज है जिसमें AB=AC है। AD बहिष्कोण PAC को समद्विभाजित करता है और CD∣∣BA है। दर्शाइए कि
(i) ∠DAC=∠BCA और
(ii) ABCD एक समांतर चतुर्भुज है।
(i) दिया है: ABC एक समद्विबाहु त्रिभुज है जिसमें AB=AC
इसलिए ∠ABC=∠ACB [बराबर भुजाओं के सम्मुख कोण]
साथ ही ∠PAC=∠ABC+∠ACB [त्रिभुज का बहिष्कोण]
या ∠PAC=2∠ACB ………..i
अब AD कोण PAC को समद्विभाजित करती है।
इसलिए ∠Pac=2∠DAC………ii
अतः 2∠DAC=2∠ACB [i और ii से]
या ∠DAC=∠ACB
(ii) अब ये दोनों बराबर कोण एकांतर कोण हैं जो रेखाखण्डों BC और AD को तिर्यक रेखा AC द्वारा प्रतिच्छेद करने से बनते हैं।
इसलिए BC∣∣AD
साथ ही BA∣∣CD [दिया है]
इस प्रकार चतुर्भुज ABCD की सम्मुख भुजाओं के दोनों युग्म समांतर है।
अतः ABCD एक समांतर चतुर्भुज है।
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - अतिलघु उत्तरीय प्रश्न (समांतर चमुर्भुज, आयत, वर्ग तथा समचतुर्भुज से संबंधित परिभाषाओं, प्रमेयों तथा उपप्रमेयों के सीधे प्रयोग पर आधारित प्रश्नः)16videos
समांतर चतुर्भुज
- BOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - लघु उत्तरीय प्रश्न4videos
समांतर चतुर्भुज
- BOOK - KC SINHACHAPTER - वृत्त EXERCISE - वस्तुनिष्ठ प्रश्न17videos
वृत्त
- BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न7videos
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
Similar Questions
रिक्त स्थानों को भरें:
कोई समांतर चतुर्भुज एक समचतुर्भुज होगा यदि और केवल यदि उसके...................... एक-दूसरे पर लम्ब हो।04:23View Solutionकिसी समांतर चतुर्भुज ABCD में ∠D=110∘ तो ∠A एवं ∠B की माप अंशों में लिखें।
02:00View Solutionवृत्त पर किन्ही दो बिन्दुओं को मिलाने वाली रेखाखंड को क्या कहते है ?
05:06View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
04:26View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
03:28View Solutionनिम्न कथन सत्य है या असत्य|
एक आव्यूह एक संख्या को निरूपित करता है ।03:22View SolutionIn triangle ABC, DE||BC where D is a point on AB and E is a point on AC. DE divides the area of triangle ABC into two equal parts.Then DB : AB is equal to एक त्रिभुज ABC DE||BC है जिसमें D,AB पर एक बिंदू है और E, AC पर एक बिंदू है। DE, triangle ABC के क्षेत्रफल को दो समान भागों में विभाजित करता है, DB : AB किसके बराबर हे?
04:37View SolutionA circle is inscribed in triangle ABC , touching AB at P, BC at Q and AC at R. If AR=5 cm, RC= 6 cm and AB=12 cm, then perimeter of triangle ABC is: एक वृत्त किसी त्रिभुज ABC में समाहित है जो AB को P पर, BC को Q पर तथा AC को R पर स्पर्श करता है | यदि AR =5 सेमी और AB = 12 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
02:11View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
03:52View SolutionIn triangle ABC , AD bisects angle A and intersects BC at D. If BC = a ,AC = b and AB = c, then BD = ? त्रिभुज ABC में, AD कोण A को समद्विभाजित करता है तथा BC को D पर काटता है | यदि BC = a, AC = b और AB = c है, तो BD = ?
02:41View Solutiontriangle ABC is a triangle, where angle B is obtuse. AD is perpendicular on CB produced at D. If AB = 8cm, BC = 7cm and BD = 4cm, then AC is equal to : ABC एक त्रिभुज है, जिसमें कोण B अधिक कोण है | AD, CB पर लम्ब है जिसे D पर डाला गया है | यदि AB =8 सेमी, BC = 7 सेमी और BD = 4 सेमी है, तो AC किसके बराबर है ?
03:31View SolutionIn triangle ABC , angle ABC=90^@ and BD bot AC . If AD = 4 cm and CD =5 cm, then BD is equal to: त्रिभुज ABC में, angle ABC=90^@ तथा BD bot AC है | यदि AD =4 सेमी और CD = 5सेमी है, तो BD किसके बराबर है ?
04:17View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=158∘. Then ∠BAC is equal to :
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इसे घेरने वाले वृत्त का व्यास है और ∠ADC=158∘ है | कोण BAC का मान ज्ञात करें |05:31View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=160∘. What is the measure of the ∠BAC ?
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इसे घेरने वाले वृत्त का व्यास है और ∠ADC=160∘ है | कोण BAC का माप क्या है ?03:50View SolutionA circle is inscribed in a quadrilateral ABCD touching AB,BC, CD and AD at the points P,Q,R and S, respectively, and ∠B=90∘. If AD = 24 cm, AB=27 cm and DR = 6cm, then what is the circumference of the circle ?
एक वृत्त चतुर्भुज ABCD के भीतर स्थित है जो AB, BC, CD और AD को क्रमशः P, Q, R और S पर स्पर्श करता है और ∠B=90∘ है | यदि AD = 24 सेमी, AB=27 सेमी और DR = 6 सेमी है, तो वृत्त की परिधि ज्ञात करें |02:51View Solution

