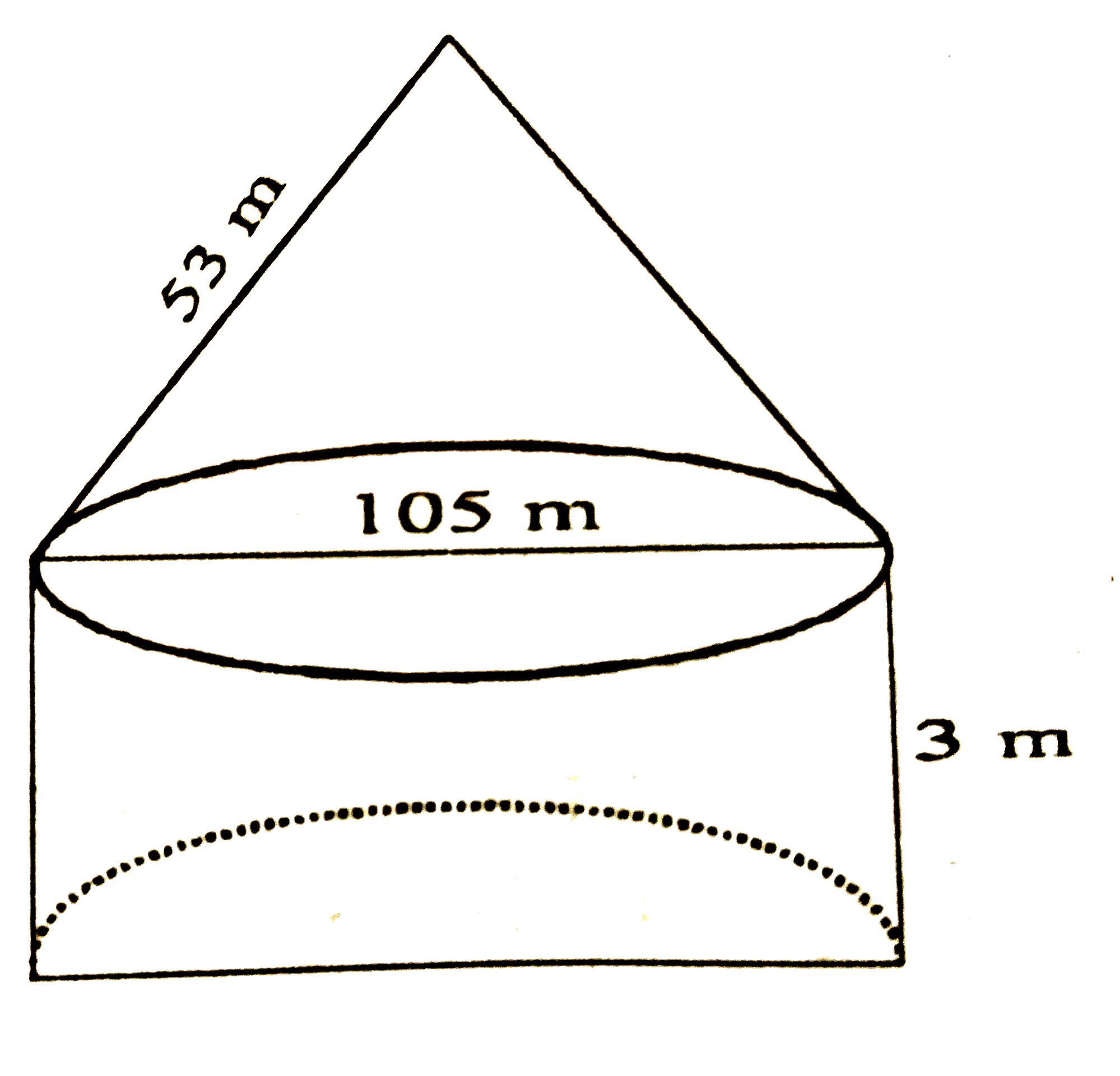
सर्कस का एक तम्बू 3 m की ऊँचाई तक तो बेलनाकार है और फिर ऊपर शंक्वाकार है यदि उसका व्यास 105 m तथा शंकु के तिरछी ऊँचाई 53 m हो, तो आवश्यक कैनवास का कुल क्षेत्रफल ज्ञात करें।
प्रश्न से,
सर्कस के तम्बू के बेलनाकार भाग की लम्बाई = 3 m
व्यास = 105 m ∴ त्रिज्या r=1052m
बेलनाकार भाग के ऊपर शंक्वाकार भाग की तिरछी ऊँचाई l=53m
तम्बू के बेलनाकार भाग का वक्र पृष्ठ =2πrh
=2×227×1057×3m2
=22×45m2=990m2
पुनः तम्बू के शंक्वाकार भाग का पृष्ठ क्षेत्रफल =πrl=227×1052×53m2
=11×15×53m2=8745m2
तम्बू का कुल पृष्ठ क्षेत्रफल =(990+8745)m2=9735m2
अतः आवश्यक कैनवस का कुल क्षेत्रफल =9735m2
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - लम्ब वृत्तीय शंकु EXERCISE - EXERCISE-1746videos
लम्ब वृत्तीय शंकु
- BOOK - KC SINHACHAPTER - लम्ब वृत्तीय शंकु EXERCISE - वस्तुनिष्ठ प्रश्न7videos
लम्ब वृत्तीय शंकु
- BOOK - KC SINHACHAPTER - लम्ब वृतीय बेलन EXERCISE - वस्तुनिष्ट प्रश्न10videos
लम्ब वृतीय बेलन
- BOOK - KC SINHACHAPTER - वास्तविक संख्याएंEXERCISE - उत्तरोत्तर आवर्धन द्वारा संख्या रेखा पर परिमेय संख्या का निरूपण देखने पर आधारित प्रश्नः3videos
वास्तविक संख्याएं
Similar Questions
किसी लम्ब बर्तुल शंकु में यदि h = 4m तथा r = 3m तो l = …………….
09:58View Solution24 मीटर ऊँचे शंकुकार तम्बू के आधार की परिधि 44 मीटर है। इस तम्बू को बनाने में प्रयुक्त कैनवास का क्षेत्रफल है :-
02:27View Solutionएक बेलन के आधार का व्यास 14 सेमी है और उसका वक्रपृष्ठ 1540 सेमी 2 है तो उसकी ऊंचाई है
01:49View Solutionउत्तरोत्तर आवर्धन द्वारा संख्या रेखा पर 2.662 को देखिए।
01:10View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
03:00View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
03:00View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
03:00View Solutionयदि शंकु की त्रिज्या 5 से. मी. हो, तो उसका व्यास होगा
05:00View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
04:05View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3, 4) और केन्द्र (2,3) हो, तो दूसरे सिरे का निर्देशांक ज्ञात कीजिए।
02:44View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3, 4) और केन्द्र (2,3) हो, तो दूसरे सिरे का निर्देशांक ज्ञात कीजिए।
04:30View Solutionपृथ्वी और चन्द्रमा का कुल द्रव्यमान 6.04×1024 किग्रा है। यदि चन्द्रमा का द्रव्यमान 7.34×1022 किग्रा है तो पृथ्वी का द्रव्यमान ज्ञात कीजिए।
02:55View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
01:44View SolutionThe lateral surface area of frustum of a right circular cone, if the area of its base is 16 pi cm^2 and the diameter of circular upper surface is 4cm and stant height 6 cm, will be किसी लम्ब वृत्ताकार शंकु के छिननक के पार्श्व सतह का क्षेत्रफल क्या होगा, जिसके आधार का क्षेत्रफल 16 pi से.मी.^2 है, वृत्ताकार उपरी सतह का व्यास 4 से.मी. है और तिरछी ऊँचाई 6 से.मी. है?
03:08View SolutionAssume that a drop of water is spherical and its diameter is one-tenth of a cm. A conical glass has a height equal to the diameter of its rim. If 32000 drops of water can fill the glass completely, then the height of the glass (in cm.) is मान लें कि पानी को एक बूंद गोलाकार है और इसका व्यास एक सेमी का दसवां हिस्सा है। एक शंक्वाकार गिलास की ऊँचाई, उसके आधार (rim) के व्यास के बराबर है। यूदि 32000 पानी की बूंदें गिलास को पूरी तरह से भर देती हैं, तो गिलास को ऊँचाई (सेमी में) कितना है?
01:34View SolutionThe heights of a cone, cylinder and hemisphere are equal. If their radii are in the ratio 2:3:1, then the ratio of the their volumes is एक शंकु, बेलन तथा गोलार्द्ध की ऊँचाई बराबर हैं। यदि उनकी त्रिज्या 2: 3: 1 के अनुपात में है, तो उनके आयतनों का अनुपात है:
03:52View Solution

