एक A.P. के प्रथम 32 पदों का योग ज्ञात करें जिसका nवाँ पद 3-2n हैं ।
The correct Answer is:-960
Step by step video, text & image solution for एक A.P. के प्रथम 32 पदों का योग ज्ञात करें जिसका nवाँ पद 3-2n हैं । by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - समांतर श्रेढ़ी EXERCISE - वस्तुनिष्ठ प्रश्न32videos
समांतर श्रेढ़ी
- BOOK - KC SINHACHAPTER - समांतर श्रेढ़ी EXERCISE - अभ्यास 5.4 (दीर्घ उत्तरीय प्रश्न)22videos
समांतर श्रेढ़ी
- BOOK - KC SINHACHAPTER - वृत्तों से संबंधित क्षेत्रफल EXERCISE - वस्तुनिष्ठ प्रश्न21videos
वृत्तों से संबंधित क्षेत्रफल
- BOOK - KC SINHACHAPTER - सांख्यिकीEXERCISE - वस्तुनिष्ठ प्रश्न35videos
सांख्यिकी
Similar Questions
यदि A.P. का nवाँ पद 3n + 5 हैं तो इसका सार्वअंतर होगा।
03:48View Solutionकिसी समान्तर श्रेणी का पाँचवाँ और पन्द्रहवाँ पद क्रमशः 13 और -17 हैं , तो इसके इक्कीस पदों का योगफल ज्ञात कीजिए ।
07:52View Solutionयदि एक अर्द्धवृत का परिमाप 36 cm हो, तो इसकी त्रिज्या है |
01:53View Solutionकेंद्रीय प्रवृत्ति की सबसे उपयुक्त माप है:
02:23View Solution(1+2x)5/2 का प्रथम ऋणात्मक पद ज्ञात कीजिए|
04:16View Solutionएक समान्तर श्रेढ़ी में पदों की संख्या सम ( even ) है| उसके विषम पदों का योग 24 तथा सम पदों का योग 30 है और अंतिम पद, प्रथम पद से 1012 अधिक है | पसं की संख्या एवं श्रेढ़ी ज्ञात कीजिए |
02:07View Solutionएक श्रेणी जिसका n वा पद nx+y है के r पदों का योगफल होगा
04:46View Solutionएक श्रेणी, जिसका n वाँ पद (nx)+y है, तब r पदों का योग होगा
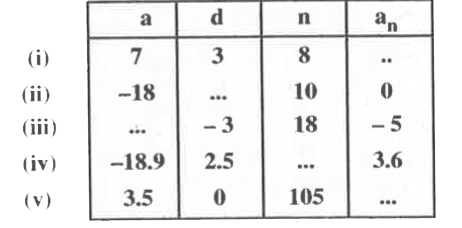
02:13View Solutionनिम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a , सार्व अंतर d और nवाँ पद a_nहै:
 45:17View Solution
45:17View Solutionदिखाइए कि अनुक्रम जिसका n वाँ पद 2n2+n+1 है, एक A.P. नहीं है।
28:39View Solution(1) किसी A.P. के प्रथम 10 पदों का योगफल ज्ञात कीजिए यदि T1=−14 और T5=20.
(ii) किसी A.P. का तीसरा पद 14 और 8वाँ पद 34 है।Sn और S30 ज्ञात कीजिए।33:07View Solutionयदि गुणोत्तर श्रेणी के अन्नत पदों का योगफल S तथा प्रथम पद a है, तो सार्वअनुपात r ज्ञात कीजिए।
49:40View Solutionसमांतर श्रेणी के प्रथम N पदों का योग
57:46View SolutionBoards 2021|समान्तर श्रेणी#!#A.P का nवाँ पद#!#Revision
View SolutionBoards 2021|समान्तर श्रेणी#!#A.P के प्रथम n पदों का क्षेत्रफल#!#Revision
42:41View SolutionRevision|A.P के प्रथम n पदों का योगफल#!#Boards 2021
48:01View Solution

