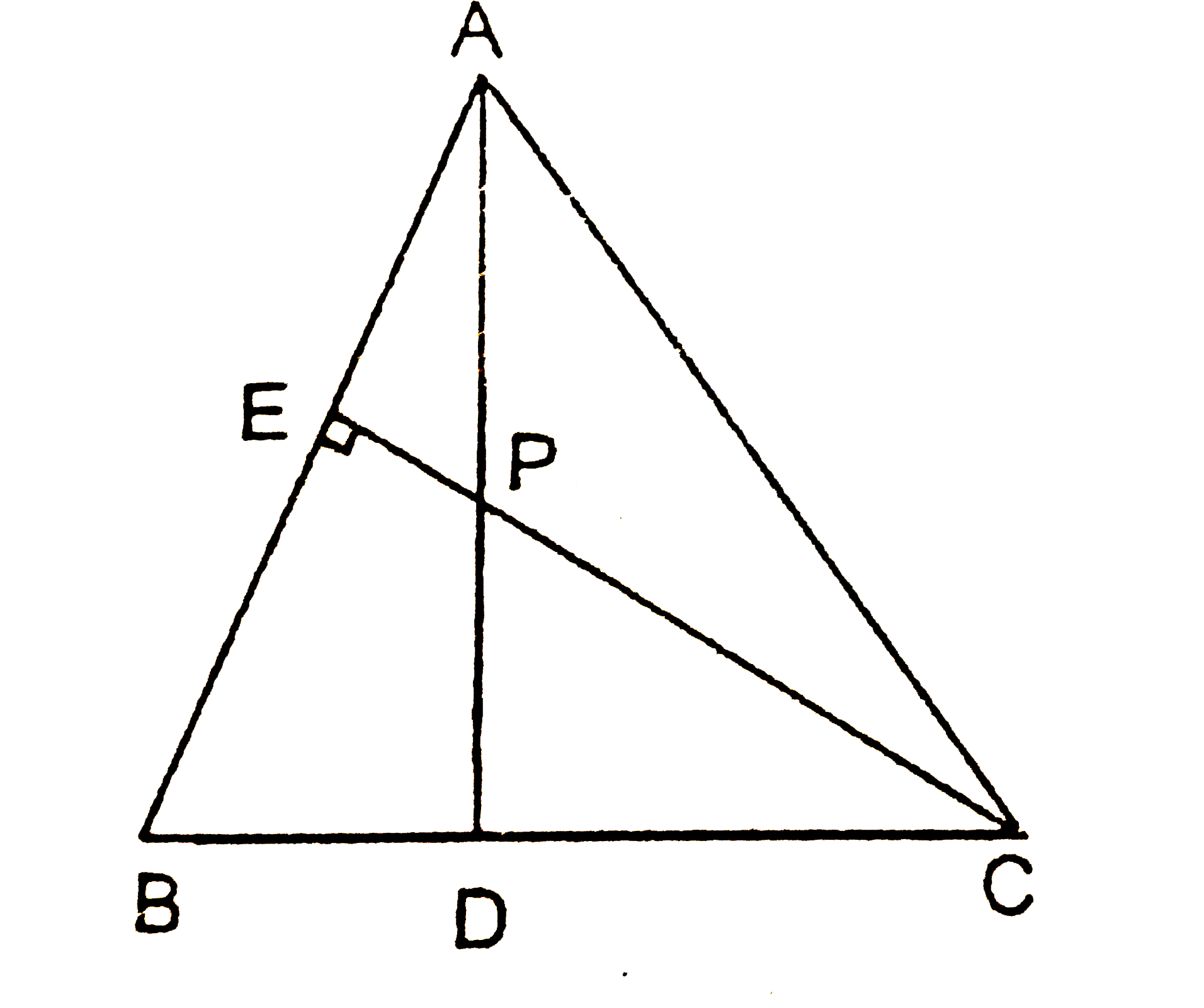
दिए गये चित्र में ΔABC के शीर्ष लम्ब AD और CE परस्पर बिन्दु P पर प्रतिच्छेद करते है । दिखाए कि :
दिया है : ΔABC के शीर्ष लम्ब AD और CE एक - दूसरे P को पर प्रतिच्छेद करते है ।
उपपत्ति : (i) ΔAEP और ΔCDPमें,
∠AEP=∠CDP(प्रत्येक=90∘)
∠APE=∠CPD (शीर्षभिमुख कोण)
ΔAEP~ΔCDP ( AA समरूपता से)
(ii) ΔABD और ΔCBE में,
∠ADB=∠CEB(प्रत्येक=90∘)
∠B=∠B (उभयनिष्ट)
∴ΔABD~ΔCBE (AA समरूपता से)
(iii) ΔAEP और ΔADB में,
∠AEP=∠ADB(प्रत्येक=90∘)
∠EAP=∠BAD (उभयनिष्ट)
अतः ΔAEP~ΔADB (AA समरूपता से)
(iv) ΔPDC और ΔBEC में,
∠PDC=∠BEC(प्रत्येक=90∘)
∠PCD=∠ECB (उभयनिष्ट)
∴ΔPDC~ΔBEC (AA समरूपता से)
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.122videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )8videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.485videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न44videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)07:39View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
06:40View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..04:56View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
05:25View Solutionसदिशों के प्रयोग द्वार सिद्ध कीजिए कि बिंदु A(−2,3,5),B(7,0,−1),C(−3,−2,−5) और D(3,4,7) इस प्रकार हैं कि AB और CD बिंदु P(1,2,3) पर प्रतिच्छेद करते हैं।
06:27View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
01:24View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
01:33View Solutionयदि किसी बिंदु P के परवलय y2=4x पर खींची गई दो स्पर्श-रेखाएँ परस्पर लम्ब हों, तो P का बिन्दुपथ है :
01:38View Solutionबिन्दु (1,1,2) से समतल 2x−2y+4z+5=0 पर डाले गये लम्ब की लम्बाई और लम्बपाद के निर्देशांक ज्ञात कीजिये।
01:30View Solutionदिये गये चित्र में स्पर्श रेखा है -
 03:43View Solution
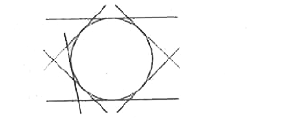
03:43View Solutionदिये गये चित्र में स्पर्श रेखाओ की संख्या है -
 06:33View Solution
06:33View Solutionदिये गये चित्र में स्पर्श रेखा है:
 03:41View Solution
03:41View Solutionदिये गये चित्र में स्पर्श रेखाओ की संख्या है:
 05:05View Solution
05:05View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
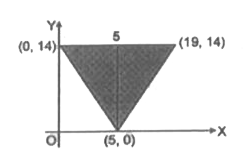
04:32View Solutionचित्र में दिखाए गए छायांकित क्षेत्र के लिए असामिका है-
 02:37View Solution
02:37View Solutionमाना PQ और RS,r त्रिज्या के वृत्त के व्यास के सिरों पर खींची गई स्पर्शियाँ है। यदि PS और RQ परिधि पर स्थिति बिन्दु X पर प्रतिच्छेद करते है तो 2r बराबर है-
04:21View Solution

