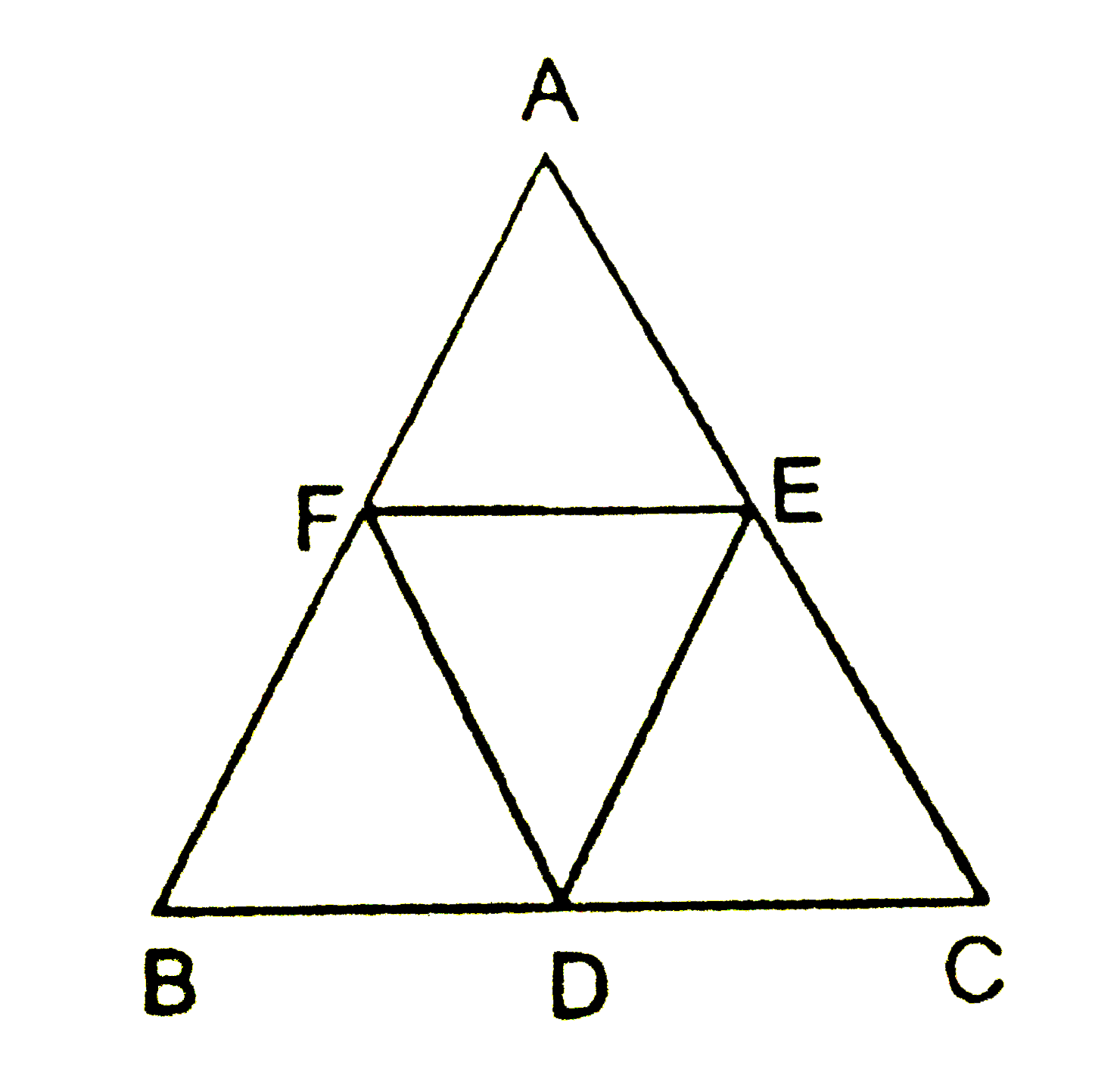
सिद्ध करें कि किसी त्रिभुज की तीनों भुजाओं के मध्य बिन्दुओं के मिलाने वाले रेखाखण्डों से बने चारों त्रिभुजों में प्रत्येक मूल त्रिभुज के समरूप होता है ।
दिया है : ΔABC में D,E,F भुजाएँ BC,CA और AB के मध्य बिन्दु है ।
सिद्ध करना है : ΔAFE~ΔABC,ΔFBD~ΔABC,ΔEDC~ΔABC
और ΔDEF~ΔABC.
उपपत्ति : F और E क्रमशः AB और AC के मध्य बिन्दु है ।
⇒FE∣∣BC
⇒∠AFE=∠B (संगत कोण)
ΔAFE और ΔABC में, ∠AFE=∠B
और ∠A=∠A (उभयनिष्ट)
∴ΔAFE~ΔABC
इसी तरह से, Δ~ΔABCऔर ΔEDC~ΔABC.
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.122videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )8videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.485videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न44videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)07:05View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
07:31View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..06:12View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
04:17View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
06:19View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
03:17View Solutionदिखाइए कि किसी त्रिभुज में भुजाओं के लम्ब अर्धक संगामी होते हैं |
04:32View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
06:40View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
52:08View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
58:11View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
42:33View Solutionरेखाओ x = 0, y = 0, 2x + 3y = 5 से बने त्रिभुज के परिवृत का समीकरण है
47:17View Solutionसमरूप त्रिभुजों के क्षेत्रफल
27:39View Solutionहीरोन के सूत्र के प्रयोग से किसी त्रिभुज का क्षेत्रफल ज्ञात करना
43:24View Solutionत्रिभुज |त्रिभुजों के प्रकार |सर्वांगसम आकृतिया |त्रिभुजों का सर्वांगसमता |सारांश
45:00View Solutionत्रिभुज|त्रिभुजों के प्रकार|सर्वांगसम आकृतियाँ|समरूप आकृतियाँ |सारांश
39:11View Solution

