सिद्ध कीजिए कि समकोण समद्विबाहु त्रिभुज की एक युग्म पर बने समबाहु त्रिभुज का क्षेत्रफल उसके विकर्ण पर बनी समबाहु त्रिभुज के क्षेत्रफल का आधा होता है ।
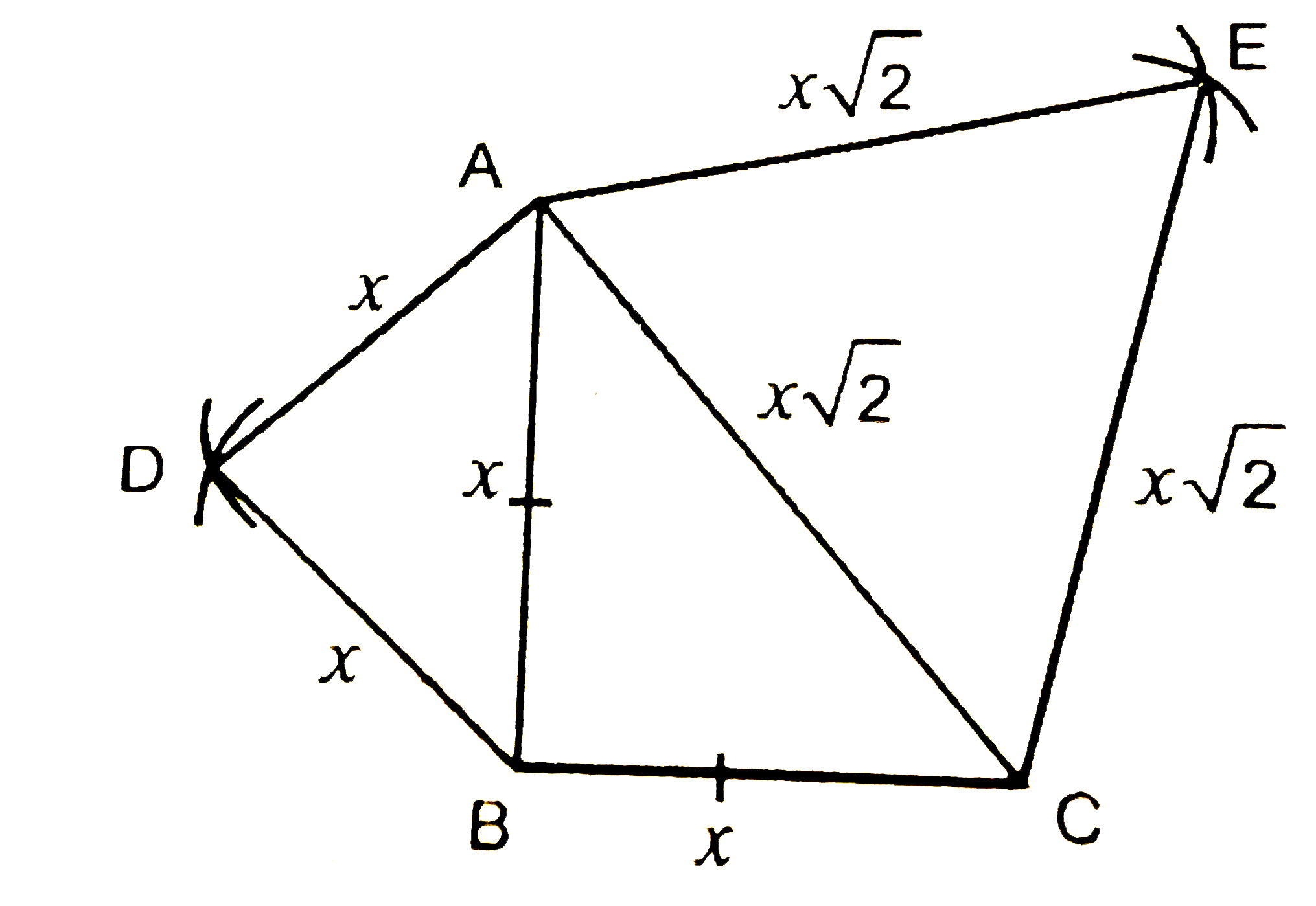
एक ΔABC है जिसमे ∠ABC=90∘ और AB=BC है । ΔABD और ΔACE समबाहु त्रिभुज है ।
सिद्ध करना है : क्षे०(ΔABD)=12क्षे०(ΔCAE)
उपपत्ति : मान कि AB=BC=x इकाई
अब CA=√AB2+AC2=√x2+x2=x√2 इकाई ΔABD और ΔCAE में , प्रत्येक कोण 60∘ है । क्योंकि ये समबाहु त्रिभुज है ।
चूँकि दो समरूप त्रिभुजों के क्षेत्रफल का अनुपात उनकी संगत भुजाओं के वर्णों के अनुपात के बराबर होता है ।
∴क्षे०(ΔABD)क्षे०(ΔCAE)=AB2CA2=x2(x√22)=x22x2=12
अतः क्षे०(ΔABD)=12क्षे०(ΔCAE) .
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.122videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )8videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.485videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न44videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)07:05View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
50:30View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..44:02View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
45:23View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
01:04:04View Solutionत्रिभुज का क्षेत्रफल | उदाहरण
39:49View Solutionत्रिभुज का क्षेत्रफल पर आधारित महत्वपूर्ण प्रश्न
50:03View Solutionदो विशेष त्रिभुज : समबाहु तथा समद्विबाहु
01:46:57View Solutionत्रिभुज का क्षेत्रफल | उदाहरण
34:41View Solutionएक त्रिभुज का क्षेत्रफल
08:24View SolutionRevision|हीरोन के सूत्र पर आधारित महत्वपूर्ण प्रश्न#!#त्रिभुज का क्षेत्रफल तथा चतुर्भुज का क्षेत्रफल
01:15View SolutionRevision|त्रिभुज का क्षेत्रफल
29:25View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
43:44View Solutionकिसी समद्विबाहु समकोण त्रिभुज का परिमाप 2012 है तब इसका क्षेत्रफल होगा -
42:54View SolutionIf the area of an equilateral triangle is 36 sqrt3 cm^2 , then the perimeter of the triangle is: यदि एक समबाहु त्रिभुज का क्षेत्रफल 36 sqrt3 वर्ग सेमी है, तो इस त्रिभुज का परिमाप कितना होगा ?
45:16View Solutionत्रिभुज का क्षेत्रफल
43:40View Solution

