दिए गये चित्र में ΔABC और ΔPQR समद्विबाहु त्रिभुज है , जिसमे ∠A=∠P यदि क्षे०(ΔABC)क्षे०(ΔPQR)=916 तो ADPS का मान ज्ञात करें।
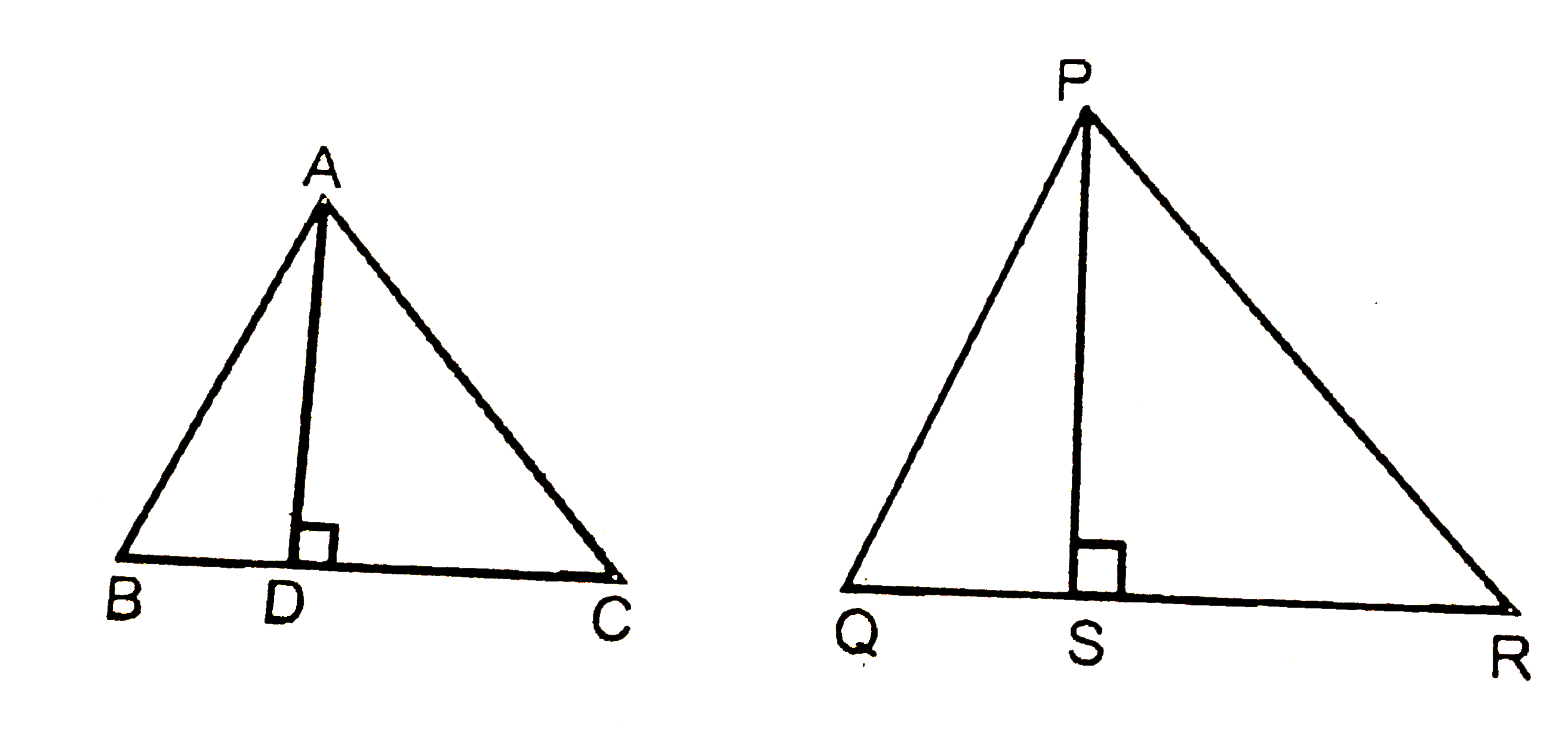
दिया है : ΔABC और ΔPQR समद्विबाहु त्रिभुज है , जिसमे ∠A=∠P और क्षे०(ΔABC)क्षे०(ΔPQR)=916
ज्ञात करना है : ADPS
चूँकि ΔABC एक समद्विबाहु त्रिभुज है (दिया है)
∴AB=AC
∴ABAC=1 ....(i)
इसी तरह से PQ=PR[∵ΔPQR एक समद्विबाहु त्रिभुज है]
∴PQPR=1
(i) और (ii) से हम जानते है कि ABAC=PQPQ
∴ABPQ=ACPR और ∠A=∠P (दिया है )
∴ΔABC~PQR(SAS समरूपता से)
ΔADC और ΔPSR में ,
∠ACD=∠PRS[∵ΔABC~ΔPQRऊपर सिद्ध किया गया है।]
∠ADC=∠PSR[प्रत्येक कोण90∘]
ΔADC~ΔPSR (AA उप -प्रमेय से)
∴ADPS=ACPR समरूप त्रिभुजों में संगत भुजाएँ समानुपाती होती है)....(iii)
किन्तु ΔABC~ΔPQR
∴BCQR=ACQR ....(iv)
(iii) और (iv) से हम पाते है ,
ADPS=BCQR
अब क्षे०(ΔABC)क्षे०(ΔPQR)=BC2QR2
(दो समरूप त्रिभुज के क्षेत्रफलों का अनुपात , उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है ।)
⇒916=BC2QR2=AD2PS2 (iv) से) ⇒ADPS=34.
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionΔPQR~ΔABC,PS⊥QR और AD⊥BC तथा PS = 4 सेमी और AD = 2 सेमी | ΔPQR तथा ΔABC के क्षेत्रफलों का अनुपात होगा :
View SolutionΔABC तथा ΔPQR में यदि ∠A=∠P,∠B=∠Q और AB=PQ तो ΔABC≅........
View Solutionयदि ΔABC~ΔADE,AB=10cm क्षे० (ΔABC)=20cm2 क्षे० (ΔDEF)=45cm2.DE का निर्धारण करें ।
View Solutionयदि ΔABC~ΔPQR,∠A=47∘,∠Q=73∘ तब ∠C=
View SolutionΔABC~ΔPQR. If A(ΔABC)=25, A(ΔPQR)=16 find AB:PQ.
View SolutionΔABC~ΔPQR. If AB:PQ=4:5, find A(ΔABC):A(ΔPQR).
View SolutionIf AD and PM be two medians of ΔABC and ΔPQR respectively, where ΔABC~ΔPQR, then prove that ABPQ=ADPM.
View SolutionΔABC~ΔPQR,∠A=32∘,∠R=65∘ then ∠B=……..
View SolutionΔABC~ΔPQR,∠A=50∘ then ∠Q+∠R=………….
View SolutionΔABC~ΔPQR,∠A+∠B=100∘, ∠R=……..
View SolutionΔABC~ΔPQR, AB:PQ=3:4 then ar ΔABC: ar ΔPQR=……
View Solution
