सिद्ध करें कि किसी समचतुर्भुज की भुजाओं पर के वर्गों का योग उसके विकर्णों पर के वर्णो के योग के बराबर होता है ।

Video Solution

Text Solution

Verified by Experts

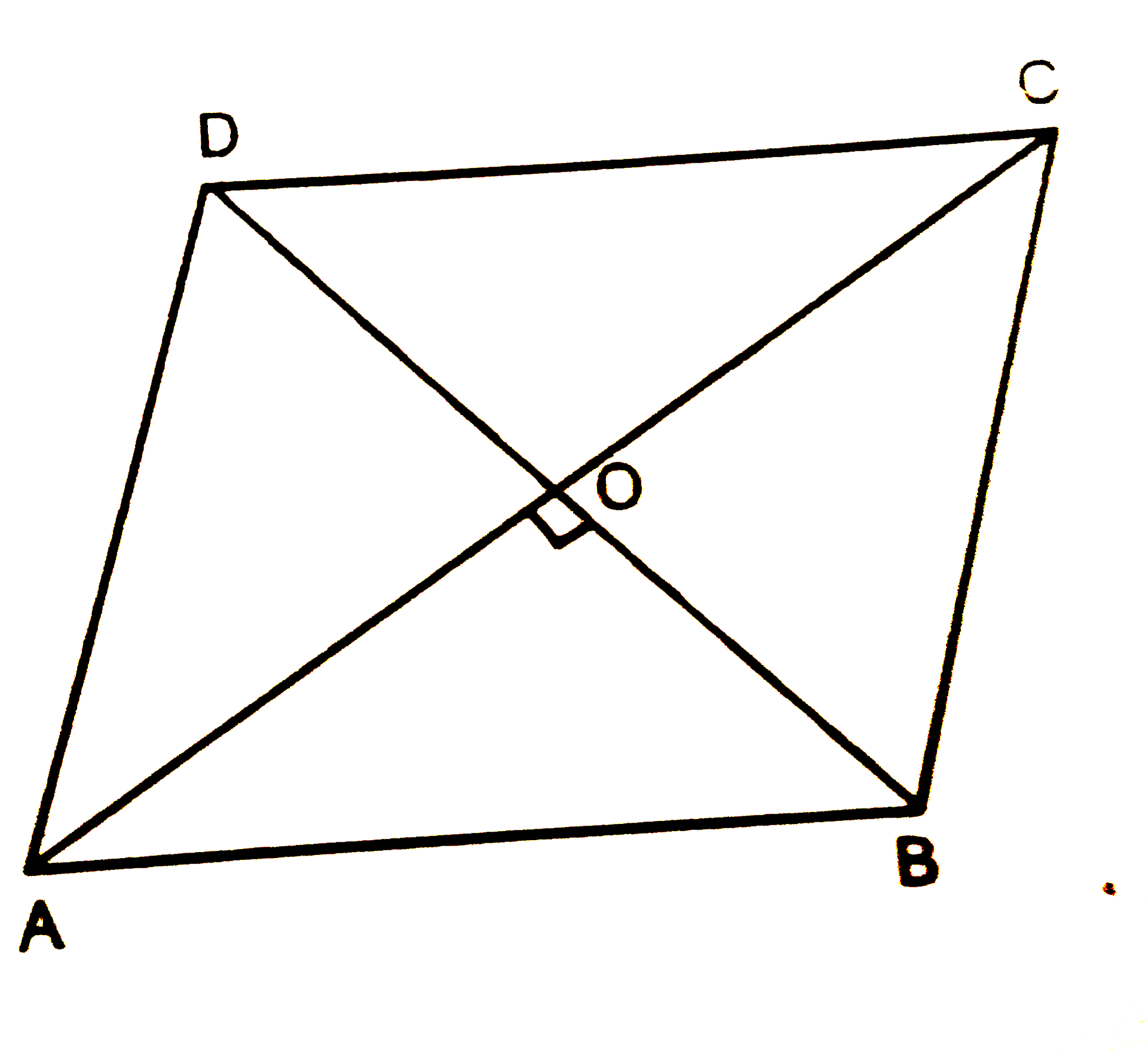
दिया है : एक समचतुर्भुज ABCD है जिसके विकर्ण ACऔर BD एक -दूसरे को O पर प्रतिच्छेद करते है ।
सिद्ध करना है : $A B^{2} + B C^{2} + C D^{2} + D A^{2} = A C^{2} + B D^{2}$
उपपत्ति : चूँकि समचतुर्भुज के विकर्ण एक -दूसरे को समकोण पर समद्विभाजीत करते है ।
$∠ A O B = ∠ B O C = ∠ C O D = ∠ D O A = 90^{\circ}, O A = \frac{1}{2} (A C) औ र O B = \frac{1}{2} (B D) Δ A O B$ में, $∠ A O B = 90^{\circ}$
$∴ A B^{2} = O A^{2} + O B^{2}$ [पाइथागोरस प्रमेय से]
$= {(\frac{1}{2} A C)}^{2} + {(\frac{1}{2} B D)}^{2} = \frac{1}{4} (A C^{2} + B D^{2})$
$∴ 4 A B^{2} = A C^{2} + B D^{2}$
किन्तु ABCD एक समचतुर्भुज है
$∴ A B = B C = C D = D A$
$∴$ (i) से , $A B^{2} + B C^{2} + C D^{2} + D A^{2} = A C^{2} + B D^{2}$
ABCD में, $A B = B C = C D = D A$ अतः ऊपर के परिणाम को इस प्रकार लिखा जा सकता है । $4 A B^{2} = A C^{2} + B D^{2}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

KC SINHA-त्रिभुज -वस्तुनिष्ठ प्रश्न

Home
Ask Doubt
Profile