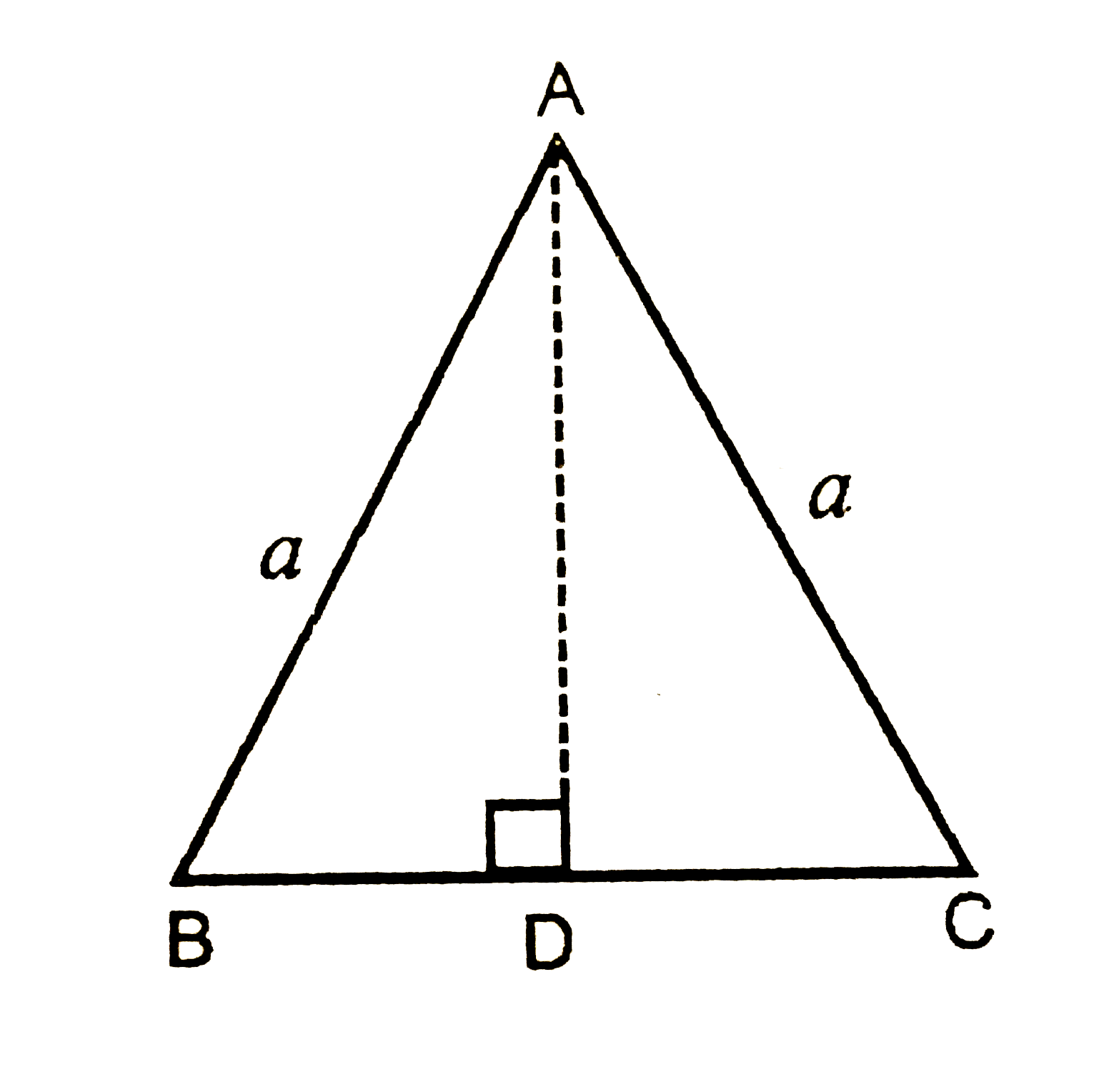
a भुजा वाले समबाहु त्रिभुज में सिद्ध करें कि (i) ऊँचाई =a√32
(ii) क्षेत्रफल =√34a2
माना कि ΔABC एक समबाहु त्रिभुज है जिसकी भुजा a है
तब AB=AC=BC=a
AD⊥BC खींचा ΔADB और ΔADC में,
AB=AC (दिया है )
∠B=∠C=60∘
और ∠ADB=∠ADC=90∘
∴ΔADB≅ΔADC
∴BD=DC=a2
(i) समकोण ΔADB से,
AB2=AD2+BD2[ पाइथागोरस प्रमेय से]
∴ AD=√AB2−BD2
=√a2−(a2)2=√a2−a24=√3a24=√32a ....(i)
अतः ऊँचाई =√32a
(ii) ΔABC का क्षेत्रफल =12× आधार × ऊँचाई =(12×BC×AD)=(12×a×√32a)=√34a2 वर्ग इकाई
अतः क्षे०(ΔABC)=√34a2 वर्ग इकाई.
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.122videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )8videos
त्रिभुज
- BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.485videos
त्रिकोणमितीय अनुपात और सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न44videos
दो चर वाले रैखिक समीकरण युग्म
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)08:11View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
01:41View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..01:31View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
07:45View SolutionIf i=sqrt(-)1, then 4+5(-(1)/(2)+(i sqrt(3))/(2))^(334)+3(-(1)/(2)+(i sqrt(3))/(2))^(365) is equal to (1)1-i sqrt(3)(2)-1+i sqrt(3)(3)i sqrt(3)(4)-i sqrt(3)
01:17View Solutionयदि sinB=12,तो सिद्ध करें कि 3cosB−4cos3B=0
03:33View Solutionयदि cosθ=√32,तो सिद्ध करें कि 3sinθ−4sin3θ=1
03:31View Solutionनिम्नलिखित करणियों को उनके परिमाण के अवरोही क्रम में लिखिए:
(i) .3√2,.6√3,.6√4, (ii) .3√3,.4√5,√2,.6√1002:54View Solution(√2+i√3)+(√2−i√3)(√3+i√2)+(√3−i√2)
03:28View Solutionसिद्ध कीजिए कि सम्मिश्र संख्याओं 0, 2i और √3+i को निरूपित करने वाले बिंदु समबाहु त्रिभुज के शीर्ष है।
02:54View Solutionसिद्ध कीजिये कि3−2√5 एक अपरिमेय संख्या है।
01:13View SolutionSimplify the following expressions: (i) (4+ √7) (3+√2) (ii) (3+√3) (5−√2) (iii) (√5−2) (√3−√5)
03:46View Solutionयदि △ABC में (If इन △ABC),a=1√6−√2,b=1√6+√2,C=60∘ तो सिद्ध कीजिए कि (Prove that) c=√42.
04:29View SolutionAn equilateral triangle of side 12 cm is drawn. What is the area (in cm^2 ) of the largest square which can be drawn inside it? 12 सेमी. भुजा वाला एक समबाहु त्रिभुज बनाया गया। इसमें बनाए जा सकने वाले बडे वर्ग को क्षेत्रफल (सेमी. में) क्या है?
04:12View SolutionThe side of an equilateral triangle is 4 cm. What is its area ?
एक समबाहु त्रिभुज की भुजा 4 cm है | उसका क्षेत्रफल कितना है?10:27View SolutionThe diagonal of a square is equal to the side of an equilateral triangle. If the area of the square is 18 sqrt 3 sq.cm. What is the area (in cm^2 ) of the equilateral triangle? किसी वर्ग का विकर्ण एक समबाहु त्रिभुज की भुजा के बराबर है | यदि वर्ग का क्षेत्रफल 18 sqrt 3 वर्ग सेमी है, तो समबाहु त्रिभुज का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें |
02:30View Solution

