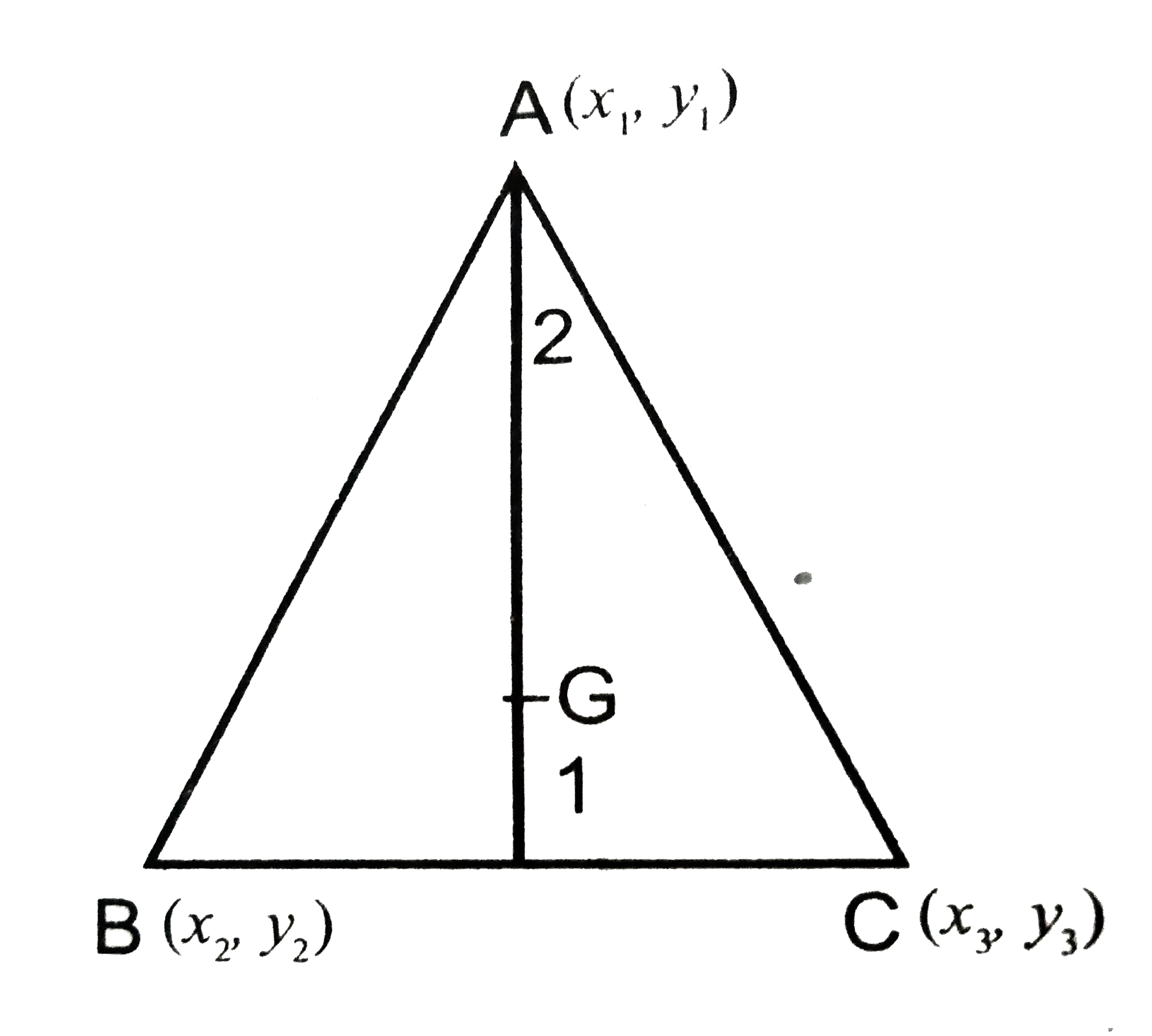
यदि A(x1,y1),B(x2,y2) और C(x3,y3)ΔABC के शीर्ष है, तो त्रिभुज के केन्द्रक का निर्देशाक ज्ञात करे |
माना कि D, BC का मध्य बिंदु है।
तब D के निर्देशांक होंगे : (x2+x32,y2+y32)
माना कि का केन्द्रक है।
हम जानते हैं कि त्रिभुज का केन्द्रक माध्यिका AD को 2:1 के अनुपात में विभाजित करता है।
∴G≡⎛⎜⎝2×x2+x32+1×x12+1,2×y2+y322+1+1×y1⎞⎟⎠
अतः G≡(x1+x2+x33,y1+y2+y33)
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - निर्देशांक ज्यामिति EXERCISE - प्रश्नावली 7.1 (अतिलघु उत्तरीय प्रश्न )13videos
निर्देशांक ज्यामिति
- BOOK - KC SINHACHAPTER - निर्देशांक ज्यामिति EXERCISE - प्रश्नावली 7.1 (लघु उत्तरीय प्रश्न )5videos
निर्देशांक ज्यामिति
- BOOK - KC SINHACHAPTER - द्विघात समीकरण EXERCISE - वस्तुनिष्ट प्रशन37videos
द्विघात समीकरण
- BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - वस्तुनिष्ट प्रश्न(Objective Questions)30videos
पृष्ठीय क्षेत्रफल और आयतन
Similar Questions
निम्नलिखित बिन्दुए किस चतुर्थेाश में स्थित है |
(10,−3)01:38View Solutionयदि किसी आयत के तीन शीर्ष (−2,0),(2,0),(2,1) है तो चौथे शीर्ष के नियामक ज्ञात कीजिए |
01:55View Solutionयदि a और b समीकरण x2−ax+b=0 के मूल है तब
05:30View Solutionएक खोखला धातुई गोला जिसकी बाह्य त्रिज्या 6cm और अन्तः त्रिज्या 4cm है को पिघलाया जाता है और इसे एक शंकु जिसके आधार की त्रिज्या 6cm है, के रूप में ढाला जाता है, तो शंकु की ऊँचाई है:
04:15View SolutionThe value of |2x1y1x1y2+x2y1x1y3+x3y1x1y2+x2y12x2y2x2y3+x3y2x1y3+x3y1x2y3+x3y22x3y3| is.
07:19View SolutionIf the points (x1,y1),(x2,y2), and (x3,y3) are collinear show that y2−y3x2x3+y3−y1x3x1+y1−y2x1x2=0
04:57View SolutionIf A(x_(1),y_(1)),B(x_(2),y_(2)) and C(x_(3),y_(3)) are the vertices of a triangle then excentre with respect to B is
06:14View SolutionIf (x_(1),y_(1)),(x_(2),y_(2)),(x_(3),y_(3)) are vertices of equilateral triangle such that (x_(1)-2)^(2)+(y_(1)-3)^(2)=(x_(2)-2)^(2)+(y_(2)-3)^(2)=(x_(3)-2)^(2)+(y_(3)-3)^(2) then
03:33View SolutionIf A(x1,y1),B(x2,y2)andC(x3,y3) are vertices of an equilateral triangle whose each side is equal to a, then prove that
∣∣ ∣ ∣∣x1y12x2y22x3y32∣∣ ∣ ∣∣ is equal toView SolutionA triangle has vertices Ai(xi,yi) for i= 1,2,3,. If the orthocenter of triangle is (0,0) then prove that
∣∣ ∣ ∣∣x2−x3y2−y3y1(y2−y3)+x1(x2−x3)x3−x1y3−y1y2(y3−y1)+x2(x3−x1)x1−x2y1−y2y3(y1−y2)+x3(x1−x2)∣∣ ∣ ∣∣=006:34View SolutionIf (x1,x2)2+(y1−y2)2=a2,(x2−x3)2+(y2−y3)2=b2(x3−x1)2+(y3−y1)2=c2. where a,b,c are positive then prove that 4∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣=(a+b+c)(b+c−a)<br>(c+a−b)(a+b−c)
06:32View Solutionअगर बिन्दुएं (x1,y2),(x2,y2) और (x3,y3) संरेखी है तब दिखायें कि y2−y3x2x3+y3,y2x3y1+y1−y2x1x2=0
04:16View SolutionIf (x1−x2)2+(y1−y2)2=a2,(x2−x3)2+(y2−y3)2=b2,(x3−x1)2(y3−y1)2=c2 and ∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣2=(a+b+c)(b+c−a)(c+a−b)(a+b−c) then the value of λ is:
04:23View SolutionIf x1,x2,x3 are in A.P. and y1,y2,y3 are in A.P. then the points (x1,y1),(x2,y2),(x3,y3)
04:59View SolutionIf =∣∣ ∣ ∣∣2ax1y12bx2y22cx3y3∣∣ ∣ ∣∣=abc2≠0then the area area of the triangle whose vertices are (x1a,y1a),(x2b,y2b),(x3c,y3c)is:
04:00View SolutionIf ∣∣ ∣ ∣∣2ax1y12bx2y22cx3y3∣∣ ∣ ∣∣=abc2≠0 , then the area of the triangle whose vertices are (x1a,y1a),(x2b,y2b)and(x3c,y3c)
06:08View Solution

