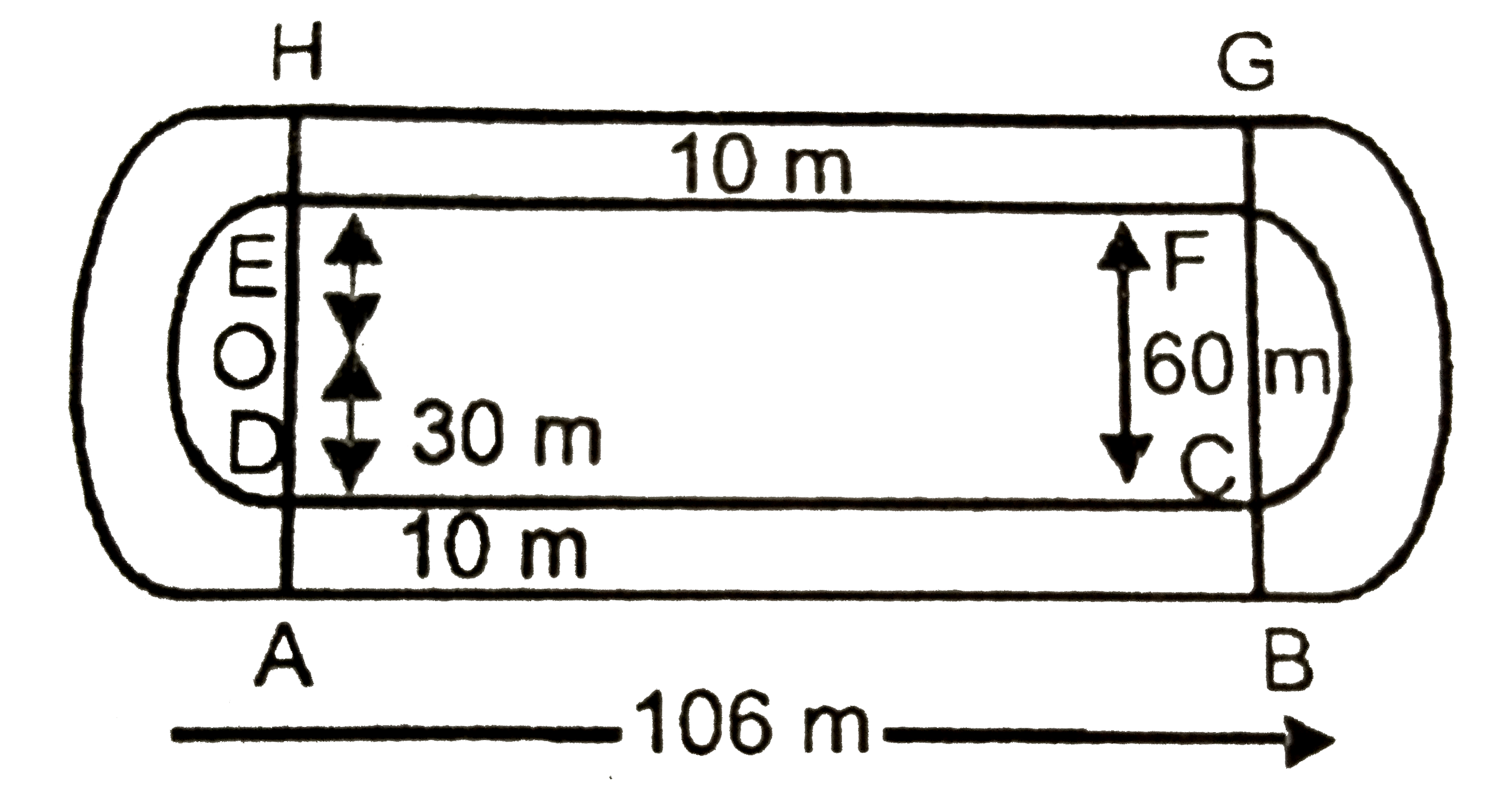
चित्र में एक दौड़ने का पथ दिखाया गया है, जिसके बाएँ और दाएँ सिरे अर्द्धवृत्ताकार है दोनों आंतरिक समांतर रेखाओं के बीच की दुरी 60m है तथा इनमे में प्रत्येक रेखाखण्ड 106m लम्बा है। यदि यह पथ 10m चौड़ा हो, तो ज्ञात कीजिये :
(i) पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में तय की गई दुरी
(ii) पथ का क्षेत्रफल।
4370m2
4340m2
4320m2
4350m2
The correct Answer is:C
दिया है कि दोनों आंतरिक समांतर रेखाखण्डो के बीच की दुरी = 60 m
प्रत्येक समांतर rekha की लम्बाई = 106 m
और पथ की चौड़ाई = 10 m
(i) पथ के आंतरिक किनारों का परिमाप = आंतरिक समांतर रेखाओं की लम्बाइयों का योग + 2 आंतरिक अर्द्धवृत्तों के सिरों का परिमाप
=(106+106)+2(π×30)
=212+2×227×30
=212+188.57=400.57cm
(ii) OD=30m तथा AD = 10 m,
∴OA=OD+DA=30+10=40m
अब, पथ का क्षेत्रफल = आयत ABCD का क्षेत्रफल + आयत EFGH का क्षेत्रफल + 2 (40 m त्रिज्या के अर्द्धवृत्त का क्षेत्रफल - 30 सेमी त्रिज्या वाले अर्द्ध वृत्त का क्षेत्रफल )
=106×10+106×10+2[12π(40)2−12π(30)2]
=2120+227(40+30)(40−30)=2120+227×70×10
=2120+2200=4320m2
अतः ट्रेक का क्षेत्रफल = 4320 m2

Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - वृत्तों से संबंधित क्षेत्रफल EXERCISE - प्रश्नावली 12.136videos
वृत्तों से संबंधित क्षेत्रफल
- BOOK - KC SINHACHAPTER - वृत्तों से संबंधित क्षेत्रफल EXERCISE - अतिलघु उत्तरीय प्रश्न19videos
वृत्तों से संबंधित क्षेत्रफल
- BOOK - KC SINHACHAPTER - वृत्त EXERCISE - वस्तुनिष्ट प्र्शन36videos
वृत्त
- BOOK - KC SINHACHAPTER - समांतर श्रेढ़ी EXERCISE - वस्तुनिष्ठ प्रश्न32videos
समांतर श्रेढ़ी
Similar Questions
एक वृत्त की परिधि , उसके व्यास से 16.8 cm अधिक है | वृत्त की परिधि ज्ञात कीजिये |
05:22View Solution7 cm त्रिज्या वाले एक त्रिज्यखण्ड का परिमाप ज्ञात कीजिए जिसका कोण 45∘ है |
04:29View Solutionयदि एक वृत्त पर जिसका केंद्र O हैं, बिंदु P से खींची गई स्पर्श रेखाएँ PA और PB एक-दूसरे से 80∘ के कोण-पर झुकी हैं, तब ∠POA बराबर हैं|
03:58View Solutionयदि A.P. का nवाँ पद 3n + 5 हैं तो इसका सार्वअंतर होगा।
05:46View Solution10 g द्रव्यमान और 50 m/s चाल वाली बंदूक की गोली एक दरवाजे में अंतः स्थापित हो जाती है । दरवाजा 1.0 M चौड़ा है और इसका द्रव्यमान 12 kg है इसके एक सिरे पर कब्जे लगे है और यह इनसे गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है । गोली के दरवाजे में अंतः स्थापन के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए ।
04:51View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
06:14View Solutionउस दीर्घवृत्ताकार पथ की यांत्रिक रचना बताइये जिसके दीर्घाक्ष की भीतरी तथा बाहरी लम्बाईयाँ क्रमानुसार 400 और 440 मीटर है । पथ की उत्केंद्रता 0.8 है पथ अंकित करने के लिए कम से कम कितनी लम्बी डोरी चाहिए ?
03:10View Solutionएक त्रिभुज , जिसके शीर्ष (0,0),(0,41) तथा (41,0) है , के आंतरिक भाग में स्थित उन बिंदुओं की संख्या जिनके दोनों निर्देशांक पूर्णांक है , है :
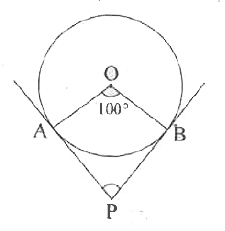
05:19View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
 04:25View Solution
04:25View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
05:21View Solutionताश के 52 पत्तो की एक सुनिश्चित गड्डी में से एक पत्ता यदृच्छया निकाला जाता है | यदि
E : निकाला गया पत्ता हुकुम का है |
F : निकाला गया पत्ता इक्का है , तो E तथा F घटनाएँ है -View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionएक शतरंज प्रतियोगिता में m पुरुष तथा दो महिलाएं भाग ले रही है । प्रत्येक प्रतिभागी (participant) दूसरे प्रत्येक प्रतिभागी के साथ दो गेम खेलता है । यदि पुरुषो के बीच आपस में खेले गए गेमों कि संख्या, पुरुष तथा महिलाओ के बीच खेले गए गेमों की संख्या से 84 अधिक है , तो m का मान है
View Solutionसूर्य और पृथ्वी के बीच की दूरी 1.496×108 km है तथा पृथ्वी और चंद्रमा के बीच की दूरी 3.84×108m है सूर्य ग्रहण होने पर चन्द्रमा पृथ्वी और सूर्य के बीच में आ जाता है इस विशेष समय पर सूर्य और चंद्रमा के बीच की दूरी क्या है ?
View Solutionरुद्धोष्म और समतापीय स्थितियों के तहत एक आदर्श गैस का उत्क्रमणीय प्रसार चित्र में दिखाया गया है | निम्नलिखित में से कौन सा कथन अशुद्ध है
View Solutionबोरेक्स में, यदि m हाइड्रॉक्सी समूहों की संख्या है और 'n', जल के अणुओं की संख्या है। m + n का योग क्या है?
View Solution

