दिये गए चित्र में ज्ञात कीजिए : (i) बिंदुओं A तथा B के बीच तुल्य - धारिता, (ii) $2 μ F$ धारिता के संधारित्र की प्लेटों के बीच विभवान्तर, (iii) $3 μ F$ धारिता के संधारित्र पर आवेश, (iv) $20 μ F$ धारिता के संधारित्र में संचित ऊर्जा तथा (v) $12 μ F$ धारिता के संधारित्र में संचित ऊर्जा ।

Video Solution

Text Solution

Verified by Experts

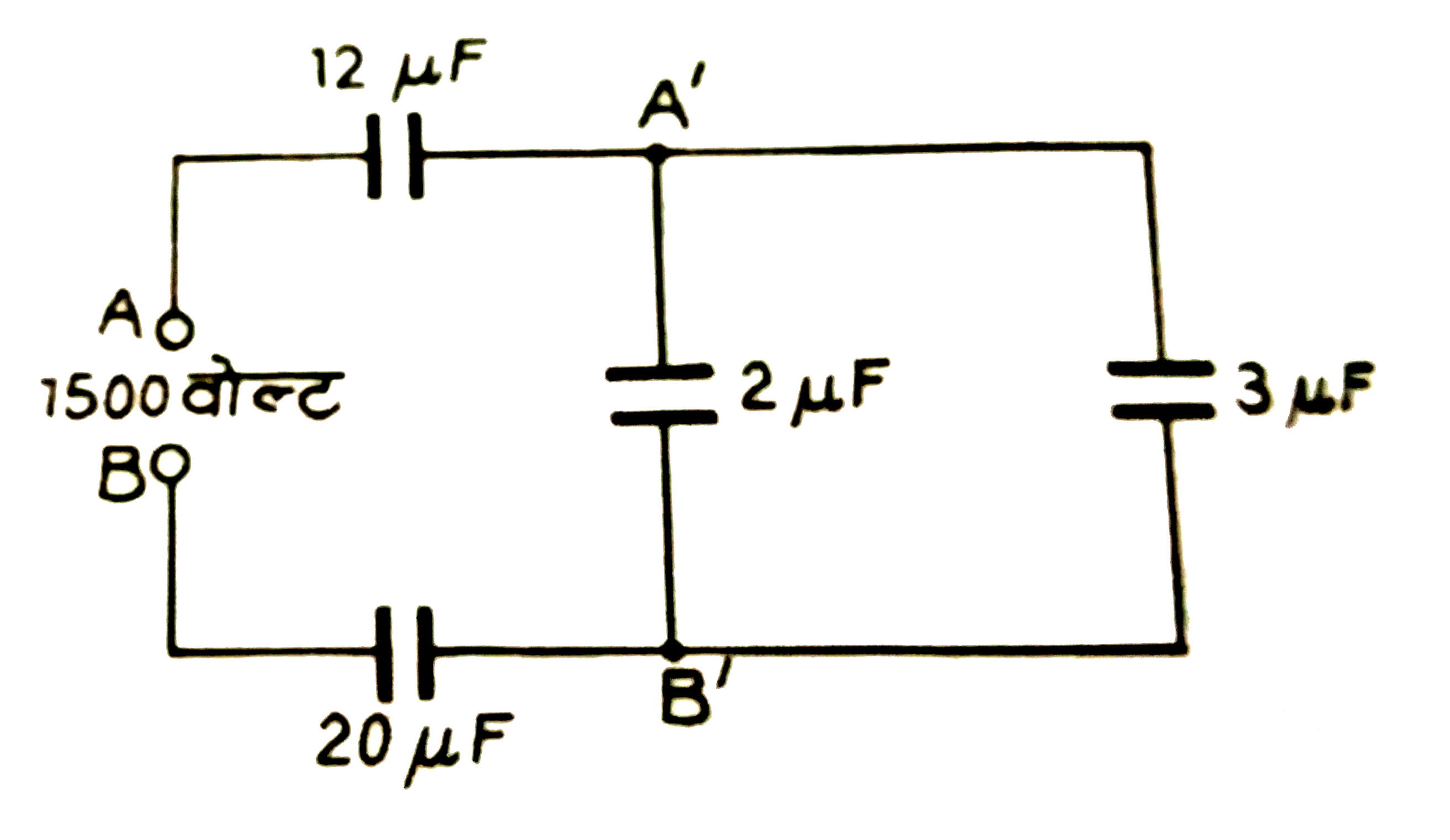
(i) संलग्न चित्र में बिंदुओं A' व B' के बीच $2 μ F$ तथा $3 μ F$ के संधारित्र समान्तर - क्रम में हैं, अतः इन बिंदुओं के बीच तुल्य - धारिता

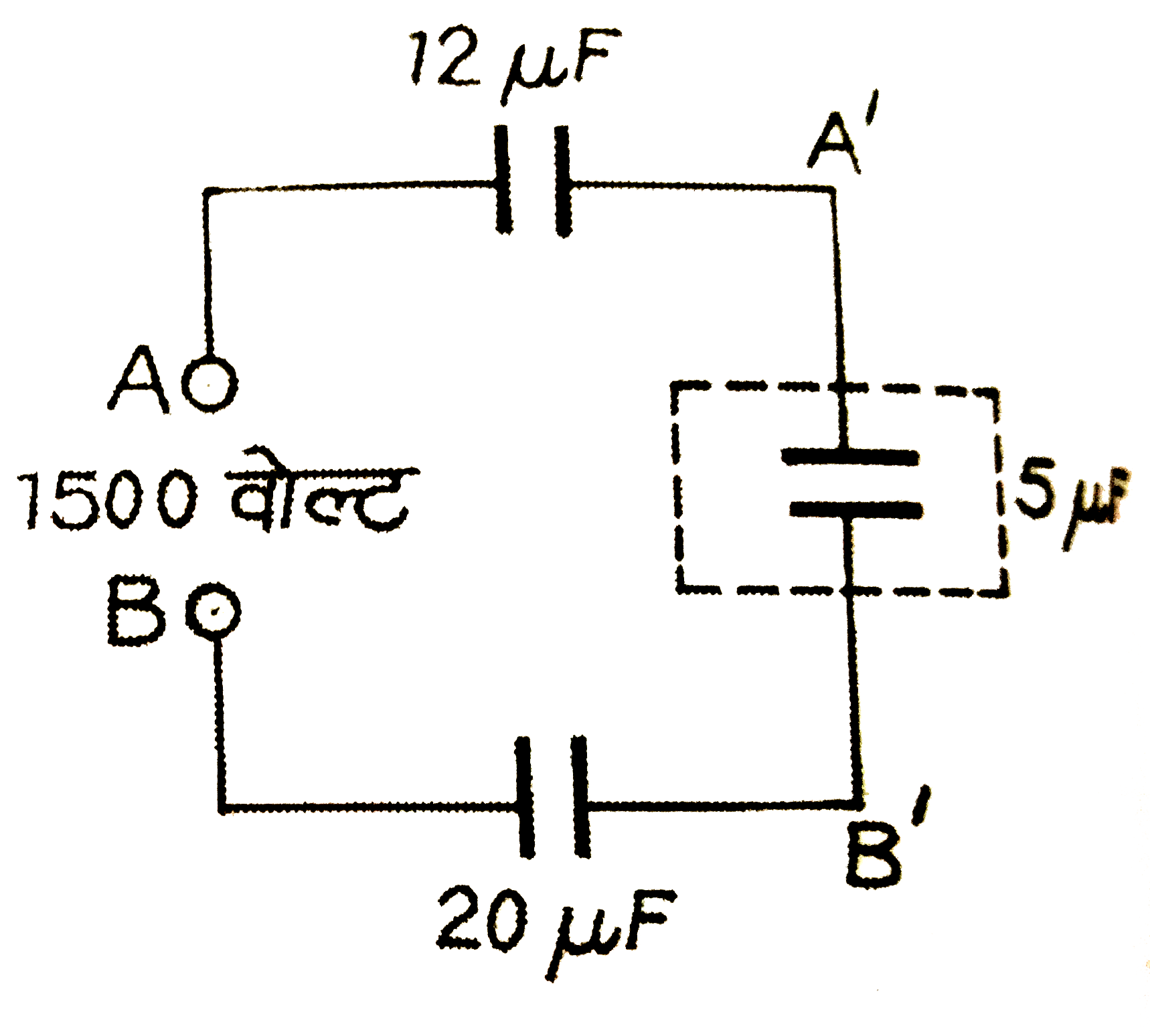
$C' = 2 μ F + 3 μ F = 5 μ F$ .
अतः अब हम यह मान सकते हैं कि बिंदुओं A व B के बीच तीन संधारित्र, जिनकी धारिताएँ क्रमशः $12 μ F, 5 μ F$ तथा $20 μ F$ हैं, श्रेणीक्रम में जुड़े हैं (संलग्न चित्र) । यदि बिंदुओं A व B के बीच तुल्य - धारिता C हो तब
$\frac{1}{C} = \frac{1}{12 μ F} + \frac{1}{5 μ F} + \frac{1}{20 μ F} = \frac{1}{3 μ F}$ .
$∴ C = 3 μ F .$
(ii) श्रेणीक्रम में जुड़े प्रत्येक संधारित्र पर आवेश
$q = C V = 3 माइक्रोफैरड \times 1500 वोल्ट$
= 4500 माइक्रोकूलॉम $(μ C)$
अतः बिंदुओं A' व B' के बीच (अर्थात तुल्य - संधारित्र $5 μ F$ की प्लेटों के बीच) विभवान्तर
$V' = \frac{q}{C'} = \frac{4500 μ C}{5 μ F} = 900$ वोल्ट |
चूँकि बिंदुओं A' व B' के बीच $2 μ F$ तथा $3 μ F$ धारिता वाले संधारित्र समान्तर - क्रम में जुड़े हैं अतः इनमे से प्रत्येक की प्लेटों के बीच वही विभवान्तर होगा जो बिंदुओं A' व B' के बीच है ।
$∴ 2 μ F$ की प्लेटों के बीच विभवान्तर V' = 900 वोल्ट ।
(iii) $3 μ F$ संधारित्र की प्लेटों के बीच विभवान्तर 900 वोल्ट है । अतः इस संधारित्र पर आवेश
$q = C माइक्रोफैरड \times 900 वोल्ट$
= 2700 माइक्रोकूलॉम $(μ C)$ |
(iv)बिंदुओं A व B के बीच विभवान्तर 1500 वोल्ट तथा तुल्य - धारिता $3 μ F$ है । अतः इन बिंदुओं के बीच तुल्य - संधारित्र पर आवेश
$q = 3 माइक्रोफैरड \times 1500 वोल्ट = 4500$ माइक्रोकूलॉम |
चूँकि बिंदुओं A व B के बीच तीन संधारित्र $12 μ F, 5 μ F$ तथा $20 μ F$ 'श्रेणीक्रम' में हैं अतः इनमे से प्रत्येक पर आवेश 4500 माइक्रोकूलॉम ही होगा । अतः $20 μ F$ संधारित्र पर आवेश
$q = 4500 माइक्रोकूलॉम = 4.5 \times 10^{- 3}$ कूलॉम|
$∴ 20 μ F$ संधारित्र में ऊर्जा
$U = \frac{1}{2} \frac{q^{2}}{C} = \frac{{(4.5 \times 10^{- 3} कूलॉम)}^{2}}{2 \times (20 \times 10^{- 6} फैरड) = 0.51}$ जूल |
(v) $12 μ F$ संधारित्र में ऊर्जा
$U = \frac{1}{2} \frac{q^{2}}{C} = \frac{{(4.5 \times 10^{- 3} कूलॉम)}^{2}}{2 \times (12 \times 10^{- 6} फैरड) = 0.84}$ जूल |

Updated on:21/07/2023

|

Class 12 PHYSICS CAPACITOR

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-संधारित्र तथा परावैद्युत -वस्तुनिष्ठ प्रकार प्रश्न

Home
Ask Doubt
Profile