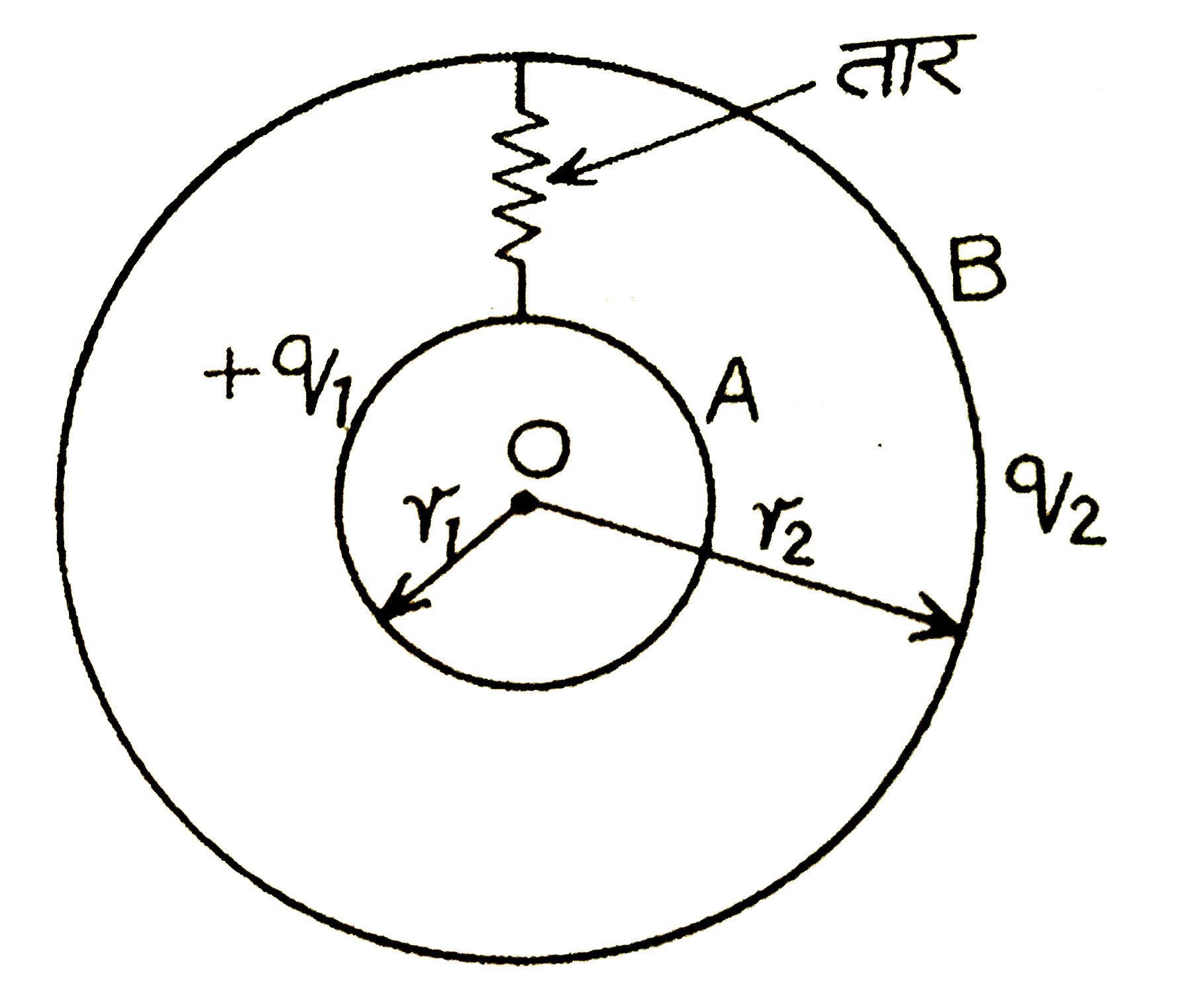
$r_{1}$ त्रिज्या तथा $q_{1}$ आवेश वाला एक छोटा गोला, $r_{2}$ त्रिज्या और $q_{2}$ आवेश के गोलीय खोल (कोश) से घिरा है। दर्शाइए यदि $q_{1}$ धनात्मक है, तो (जब दोनों को एक तार द्वारा जोड़ दिया जाता है) आवश्यक रूप से आवेश, गोले से खोल की तरफ ही प्रवाहित होगा, चाहे खोल पर आवेश $q_{2}$ कुछ भी हो।

Video Solution

Text Solution

Verified by Experts

माना $r_{1}$ त्रिज्या का एक गोलीय चालक A है जिस पर $+ q_{1}$ आवेश है। यह $r_{2}$ त्रिज्या के एक गोलीय कोश B से घिरा है जिस पर आवेश $q_{2}$ है। गोले पर वितरित है। गोले पर वितरित आवेश को इसके केंद्र पर केंद्रित मान सकते है।
गोले A का विभव $V_{A} = \frac{1}{4 π ε_{0}} [\frac{q_{1}}{r_{1}} + \frac{q_{2}}{r_{2}}]$
गोले B का विभव $V_{B} = \frac{1}{4 π ε_{0}} [\frac{q_{2}}{r_{2}} + \frac{q_{1}}{r_{2}}]$
गोले A तथा B की बीच विभवांतर $V_{A} - V_{B} = \frac{q_{1}}{4 π ε_{0}} [\frac{1}{r_{1}} - \frac{1}{r_{2}}]$
अत: स्पष्ट है कि:
(i) $V_{A} - V_{B}$ कोश B के आवेश पर निर्भर नहीं करता है, चाहे वह धनावेशित है, ऋणावेशित हो अथवा अनावेशित
(ii) $(V_{A} - V_{B}) > 0$ यदि $q_{1}$ धनात्मक है तथा $r_{2} > r_{1}$ तो $V_{A} > V_{B}$
अर्थात भीतरी गोला सदैव उच्च विभव पर रहता है अत: आवेश भीतरी गोले से बाहरी गोले की ओर प्रवाहित होगा।

|

Updated on:21/07/2023

Class 12 PHYSICS CAPACITOR

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-संधारित्र तथा परावैद्युत -अतिरिक्त प्रश्न

Home
Ask Doubt
Profile