निम्नलिखित में दिए गए प्रत्येक आव्यूहों के व्युत्क्रम (जिनका अस्तित्व हो) ज्ञात कीजिए।
⎡⎢⎣10033052−1⎤⎥⎦
माना A=⎡⎢⎣10033052−1⎤⎥⎦
⇒|A|=∣∣
∣∣10033052−1∣∣
∣∣
=1(−3−0)−0+0
(R1से विस्तार करने पर)
=−3≠0
∴A−1 का अस्तित्व है।
A11=(−1)2(−3−0)=−3,A12=(−1)3(−3−0)=3
A13=(−1)4(6−15)=−9
A21=(−1)3(0−0)−0,A22=(−1)4(−1−0)=−1
A23=(−1)5(2−0)=−2
A31=(−1)4(0−0)=0,A32=(−1)5(0−0)=0
A33=(−1)6(3−0)=3
∴adjA=⎡⎢⎣−33−90−1−2003⎤⎥⎦'=⎡⎢⎣−3003−10−9−23⎤⎥⎦
अब A−1=1|A|.adjA=1−3⎡⎢⎣−3003−10−9−23⎤⎥⎦
Topper's Solved these Questions
- सारणिकBOOK - NOOTAN HINDICHAPTER - सारणिकEXERCISE - प्रश्नावली 4.6
15 Videos
- सारणिकBOOK - NOOTAN HINDICHAPTER - सारणिकEXERCISE - विविध प्रश्नावली
19 Videos
- सारणिकBOOK - NOOTAN HINDICHAPTER - सारणिकEXERCISE - प्रश्नावली 4.4
5 Videos
- सम्बन्ध एवं फलन BOOK - NOOTAN HINDICHAPTER - सम्बन्ध एवं फलन EXERCISE - विविध प्रश्नावली
19 Videos
Similar Questions
निम्नलिखित प्रश्न दी गई समीकरण निकायों का संगत अथवा असंगत के रूप में वर्गीकरण कीजिए-
2x−y=5,x+y=4
View Solutionसिद्ध कीजिए कि सारणिक ∣∣ ∣∣xsinθcosθ−sinθ−x1cosθ1x∣∣ ∣∣,θ से स्वतंत्र है।
View Solutionनिम्नलिखित सारणिकों के अवयवों के उपसारणिक एवं सहखण्ड लिखिए।
(i) ∣∣∣2−403∣∣∣ (ii) ∣∣∣acbd∣∣∣
View Solutionमान लीजिए कि f:R→R,f(x)=10x+7 द्वारा परिभाषित फलन है । एक ऐसा फलन g:R→R ज्ञात कीजिए जिसके लिए gof=fog=IR हो ।
View SolutionThe inverse of the matrix ⎡⎢⎣10033052−1⎤⎥⎦ is
View SolutionA−1 ज्ञातकीजिए⎡⎢⎣10033052−1⎤⎥⎦
View SolutionA−1 ज्ञात कीजिए: A=⎡⎢⎣10033052−1⎤⎥⎦
View SolutionFind the inverse of each of the matrices (if it exists )
⎡⎢⎣10033052−1⎤⎥⎦
View SolutionFind the inverse of each of the matrices (if it exists )
⎡⎢⎣10033052−1⎤⎥⎦
View SolutionFind the inverse of the following
A=⎡⎢⎣10033052−1⎤⎥⎦
View SolutionThe given matrix [[1,0,0],[3,3,0],[5,2,-1]] Find out the inversions that exist.
View SolutionThe inverse of the matrix ⎡⎢⎣10033052−1⎤⎥⎦ is
View Solutionनिम्नलिखित आकृतियों में x के मान ज्ञात कीजिए
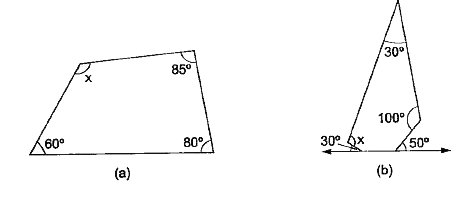
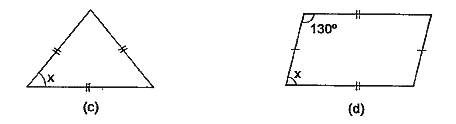
View Solutionनिम्नलिखित आकृतियों में x के मान ज्ञात कीजिए

View SolutionFind the inverse of the matrix (if it exists): ⎡⎢⎣10033052−1⎤⎥⎦
View SolutionFind the inverse of the matrix (if it exists): ⎡⎢⎣10033052−1⎤⎥⎦
View Solution
