मान लीजिए A=⎡⎢⎣1−21−231115⎤⎥⎦ हो तो सत्यापित कीजिए कि
((A')')=A
A=⎡⎢⎣1−21−231115⎤⎥⎦
∴|A|=∣∣
∣∣1−21−231115∣∣
∣∣
=1(15−1)−(−2)(−10−1)+1(−2−3)
=14−22−5=−13≠0
A11=14,A12=11,A13=−5
A21=11,A22=4,A23=−3
A31=−5,A32=−3,A33=−1
∴adjA=⎡⎢⎣1411−5114−3−5−3−1⎤⎥⎦=⎡⎢⎣1411−5114−3−5−3−1⎤⎥⎦
और A−1=1|A|.adjA=−113⎡⎢⎣1411−5114−3−5−3−1⎤⎥⎦
=⎡⎢
⎢
⎢
⎢⎣−1413−1113512−1113−413313513313113⎤⎥
⎥
⎥
⎥⎦ ltbr (i) माना B=adjA=⎡⎢⎣1411−5114−3−5−3−1⎤⎥⎦
⇒|B|=∣∣
∣∣1411−5114−3−5−3−1∣∣
∣∣
=14(−4−9)−11(−11−15)−5(−33+20)
=−182+286+65=169≠0
B11=−13,B12=26,B13=−13
B21=26,B22=−39,B23=−13
B31=−13,B32=−13,B33=−65
∴adjB=⎡⎢⎣−1326−1326−39−13−13−1365⎤⎥⎦=⎡⎢⎣−1326−1329−39−13−13−13−65⎤⎥⎦
और B−1=1|B|adjB=1169⎡⎢⎣−1326−1326−39−13−13−13−65⎤⎥⎦
=113⎡⎢⎣−12−12−3−1−1−1−5⎤⎥⎦
माना C=A−1=⎡⎢
⎢
⎢
⎢⎣−1413−1113513−1113−413313513313113⎤⎥
⎥
⎥
⎥⎦
C11=−13169=−113,C12=26169=213
C13=−13169=−113
C21=26169=213,C22=39169=−313
C23=−13169=−113
C31=−13169=−113,C32=−13169=−113
C33=−65169=−513
∴adjC=adjA−1=⎡⎢
⎢
⎢
⎢⎣−113213−113213−313−113−113−113−513⎤⎥
⎥
⎥
⎥⎦
=⎡⎢
⎢
⎢
⎢⎣−113213−113213−313−113−113−113−513⎤⎥
⎥
⎥
⎥⎦
=113⎡⎢⎣−12−12−3−1−1−1−5⎤⎥⎦=B−1−(adjA)−1
(ii) ∣∣A−1∣∣=−1413(−4169−9169)
+1113(−11169−15169)
+513(−33169+20169)
=−113
∴(A−1)−1=1|A−1|.adjA−1
=1−113.113⎡⎢⎣−12−12−3−1−1−1−5⎤⎥⎦
=⎡⎢⎣1−21231−115⎤⎥⎦=A
Topper's Solved these Questions
Similar Questions
निम्नलिखित प्रश्न दी गई समीकरण निकायों का संगत अथवा असंगत के रूप में वर्गीकरण कीजिए-
2x−y=5,x+y=4
View Solutionमान लीजिए कि f:R→R,f(x)=10x+7 द्वारा परिभाषित फलन है । एक ऐसा फलन g:R→R ज्ञात कीजिए जिसके लिए gof=fog=IR हो ।
View SolutionLet A=⎡⎢⎣1−21−231115⎤⎥⎦. Verify that ltbtgt (i) [adjA]−1=adj(A−1)
(ii) (A−1^(−1)=A
View Solutionयदि A=⎡⎢⎣1−21−231115⎤⎥⎦ हो, तो सत्यापित कीजिएः −(adjA)−1=adjA−1.
View Solutionमान लीजिए A=[1−211] हो तो सत्यापित कीजिए कि
(AdjA)−1=Adj(A−1)
View Solutionमान लीजिए A=[1−2−23] हो तो सत्यापित कीजिए कि
(A−1)−1=A.
View Solutionयदि 3+5r+7r2+……..∞=449 हो ,तो r का मान ज्ञात कीजिए ।
View Solutionआकृति के अनुसार यदि ∠BAC=80∘ हो तो ∠BCP का मान ज्ञात कीजिए।
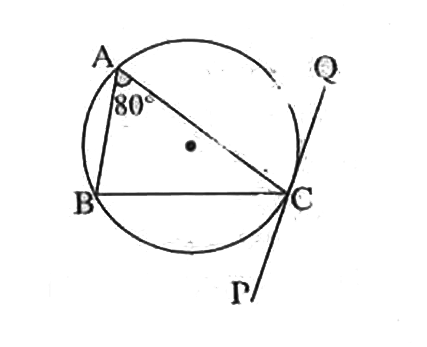
View Solutionयदि ∣∣∣4121∣∣∣2=∣∣∣321x∣∣∣−∣∣∣x−3−21∣∣∣हो तो x का मान है-
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=(2x−1)2+3
View Solutionनिम्नलिखित फलनों के उच्चतम मान तथा निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
y=−(x−1)2+10
View Solutionनिम्नलिखित फलनों के अधिकतम था निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
|sin4x+3|
View Solutionनिम्नलिखित फलनों के अधिकतम था निम्नतम मान, यदि कोई हो, तो ज्ञात कीजिए -
sin2x+5
View SolutionLet A = ⎡⎢⎣121231115⎤⎥⎦ Verify that (A^(-1) )^(-1) =A
View SolutionLet A=⎡⎢⎣1−21−231115⎤⎥⎦ Verify that
[adjA]−1=adj(A−1)
View Solution
