क्या एक ऐसे फलन का अस्तित्व है, जो प्रत्येक बिंदु, पर सतत हो किन्तु केवल दो बिंदुओं पर अवकलनीय न हो ? आपने उत्तर का औचित्य भी बतलाइए ।
हाँ
f(x)=|x−1|+|x−2|
यह फलन x के सभी वास्तविक मानों लिये सतत है
परन्तु x = 1 और x = 2 पर अवकलनीय नहीं है।
x = 1 पर
f(1)=|1−1|+|1−2|=0+1=1
L.H.L.=limx→1−f(x) मानाx=1−h
=limh→0f(1−h) ⇒1−h⇒1
=limh→0|1−h−1|+|1−h−2| ⇒ h→0
=0+|−1|=1
R.H.L.=limx→1+f(x) मानाx=1+h
=limh→0f(1+h) ⇒1+h→1
=limh→0|1+h−1|+|1+h−2| ⇒ h→0 ltBrgt =0+|−1|=1
∵ L.H.L.=f(1)=R.H.L.
∴ f(x),x=1 पर सतत है।
x = 2 पर
f(2)=|2−1|+|2−2|=1+0=1
L.H.L.=limx→2−f(x) माना 2−h+x
=limh→0f(2−h) ⇒2−h→2
=limh→0|2−h−1|+|2−h−2| ⇒ h→0
=1+0=1
R.H.L=limx→2+f(x) माना 2+h=x
=limh→0f(2+h) ⇒2+h→2
=limh→0|2+h−1|+|2+h−2| ⇒ h→0
=1+0=1
∵L.H.L.=f(2)=R.H.L
∴f(x),x=2 पर सतत है।
अब f(x)=|x−1|+|x−2|
=⎧⎪⎨⎪⎩−(x−1)−(x−2)=−2x+3यदि x<1(x−1)−(x−2)= 1यदि 1≤x≤2(x−1)+(x−2)= 2x−3यदि x>2
x = 1 पर
Lf'(1)=limh→0f(1−h)−f(1)−h
=limh→0−2(1−h)+3−1−h
=limh→02h−h=limh→0(−2)=−2
Rf'(1)=limh→0f(1+h)−f(1)h
=limh→01−1h=limh→0(0)=0
∵Lf'(1)≠Rf'(1)
∴f(x),x=1 पर अवकलनीय नहीं है।
x = 2 पर
Lf'(2)=limh→0f(2−h)−f(2)−h
=limh→01−(2×2−3)−h=limh→0(0)=0
Rf'(2)=limh→0f(2+h)−f(2)h
=limh→02(2+h)−3−1h
=limh→02hh=limh→02=2
∴Lf'(2)≠Rf'(2)
∴f(x),x=2 पर अवकलनीय नहीं है।
Topper's Solved these Questions
- सततता और अवकलनीयता BOOK - NOOTAN HINDICHAPTER - सततता और अवकलनीयता EXERCISE - एन० सी० ई० आर० टी० (प्रश्नावली 5.8)
6 Videos
- रैखिक प्रोग्रामन BOOK - NOOTAN HINDICHAPTER - रैखिक प्रोग्रामन EXERCISE - प्रश्नावली (विविध प्रश्नावली )
10 Videos
- सदिश एवं सदिशों का गुणन BOOK - NOOTAN HINDICHAPTER - सदिश एवं सदिशों का गुणन EXERCISE - विविध प्रश्नावली
19 Videos
Similar Questions
फलन f(x)=x2+2x−8,x∈[−4,2] के लिए रोले के प्रमेय को सत्यापित कीजिए।
View Solutionएक आहारविद दो भोज्यों P और Q का उपयोग करते हुए एक विशेष आहार तैयार करता है । भोज्य P का प्रत्येक पैकेट (जिसमे 30 ग्राम अंतव्रिष्ट है) में कैल्शियम के 6 मात्रक और विटामिन A के 6 मात्रक अंतव्रिष्ट हैं जबकि उसी मात्रक के भोज्य Q के पैकेट में कैल्शियम तत्व के 3 मात्रक, लौह-तत्व के 20 मात्रक, कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अंतव्रिष्ट हैं । आहार में कम-से कम 240 मात्रक कैल्शियम, लौह-तत्व के कम-से-कम 460 मात्रक और कोलेस्ट्रोल के अधिक-से-अधिक 300 मात्रक अपेक्षित हैं । आहार में विटामिन A के मात्रा का अधिकतमीकरण करने के लिए प्रत्येक भोज्य के कितने पैकेटों का उपयोग होना चाहिए? आहार में विटामिन A की अधिकतम मात्रा क्या है?
View SolutionXY - तल में x - अक्ष की धनात्मक दिशा के साथ वामावर्त दिशा में 30∘ का कोण बनाने वाला मात्रक सदिश लिखिए ।
View Solutionनिम्नलिखित कथनो में से सत्य असत्य लिखिए और अपने उत्तर का औचित्य भी दीजिए।
किसी रेखा से समान दूरी पर स्तिथ बिन्दुओ का समुच्चय एक रेखा होती है।
View Solutionनिम्नलिखित कथनो में से सत्य असत्य लिखिए और अपने उत्तर का औचित्य भी दीजिए।
एक वृत्त उन बिन्दुओ का बिन्दुपथ है जो किसी दिए गए बिंदु से नियत दूरी पर स्तिथ है।
View Solutionनिम्न में से प्रत्येक कथन सत्य या असत्य है लिखिए और उत्तर का कारण भी लिखिए।
किसी वृत्त की स्पर्श रेखा वह है जो वृत्त को दो बिंदु पर प्रतिच्छेद करती है।
View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
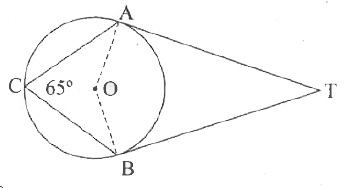
View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -

View Solutionनिम्न कथन सत्य है अथवा असत्य-
यदि सुसंगत क्षेत्र के दो कोनीय बिंदुओं पर इष्टतमकारी मान समान हो अर्थात दोनों बिंदुओं के लिए उद्देश्य फलन का मान या तो उच्चतम या निम्नतम हो तब इन बिंदुओं को मिलाने वाली रेखा पर किसी भी बिंदु के लिए उद्देश्य फलन का इष्टतमकारी मान प्राप्त होता है।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
यदि कोई ऐसे बिंदु निश्चित करना संभव न हो, जहाँ समस्या का अनुकूलतम हल हो, तो समस्या का हल अपरिवद्ध होता है।
View Solutionमाना O(0,0) तथा A(0,1) दो निश्चित बिंदु है, तो ऐसे बिंदु P जिनके लिए ΔAOP का परिमाप 4 हो, का बिन्दुपथ है
View Solutionm का वह मान, जिसके लिए फलन
f(x)={mx2x≤12xx>1 x=1 पर अवकलनीय हो है
View SolutionAB एक ऊर्ध्वाधर खंभा है, जिनका A सिरा जमीन पर है | C, AB का मध्य-बिंदु है और P जमीन पर एक बिंदु है | BC, बिंदु P पर β कोण बनता है | यदि AP = nAB हो, तो tanβ का मान है |
View Solutionयदि संख्या 354Y2, 6 का एक गुणज है तो Yअंक का मान क्या हो सकता है?
View Solutionसमाज के स्तर पर क्या न होने का अँधेरा है ?
View Solution
