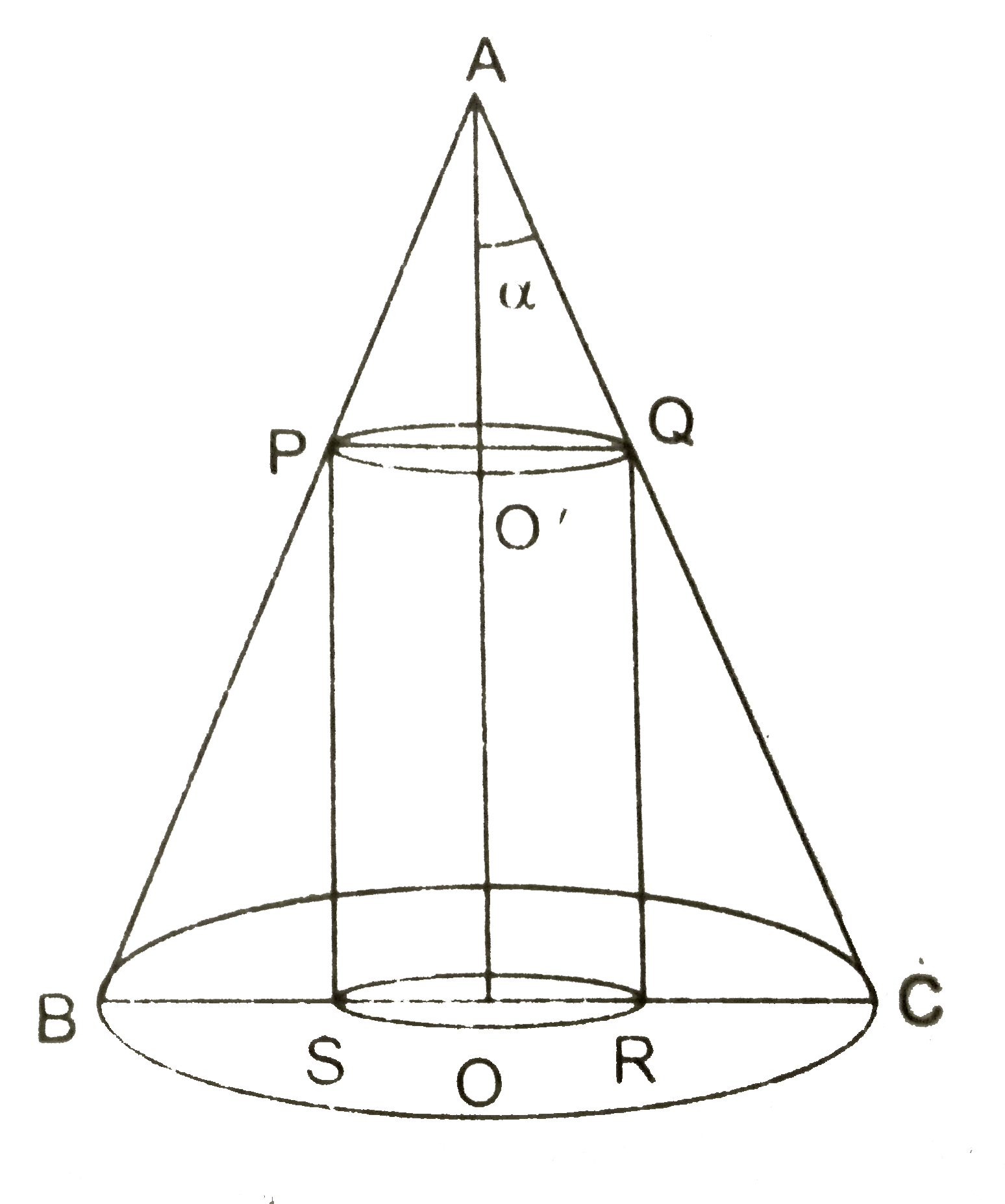
सिद्ध कीजिए कि शंकु के अंतर्गत बने लंबवृत्तीय बेलन का वाकरपृष्ठ महत्तम तब होगा जब उसकी त्रिज्या शंकु कि त्रिज्या कि आधी होगी.
माना शंकु की ऊंचाई h और अर्धशिर्ष कोण है.
माना बेलन की त्रिज्या x है.
बेलन की ऊंचाई =OO
बेलन का वाकरपृष्ठ
उच्चिष्ठ/निमनिष्ठ के लिये
जहाँ r शंकु की त्रिज्या है.
और
का मान महत्तम है.
अतः बेलन का वक्र-पृष्ठ महत्तम होगा यदि अर्थात बेलन की त्रिज्या, शंकु की त्रिज्या की आधी है.
Topper's Solved these Questions
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6.1
18 Videos
- अवकलन के अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - अवकलन के अनुप्रयोग EXERCISE - प्रश्नावली 6.2
19 Videos
- अवकल समीकरण BOOK - NOOTAN HINDICHAPTER - अवकल समीकरण EXERCISE - विविध प्रश्नावली
18 Videos
- आव्यूह BOOK - NOOTAN HINDICHAPTER - आव्यूह EXERCISE - विविध प्रश्नावली
15 Videos
Similar Questions
वृत्त के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या r के सापेक्ष ज्ञात कीजिए जबकि
(a)r=3सेमी है
(b)r=4सेमी है
View Solutionसिद्ध कीजिए R पर f(x)=3x+17 से प्रदत्त फलन निरंतर वृद्धिमान है.
View Solutionनिम्नलिखित अवकल समीकरणों में से प्रत्येक की कोटि एवं घात (यदि परिभाषित हो) ज्ञात कीजिए।
(i) d2ydx2+5x(dydx)2−6y=logx
(ii) (dydx)3−4(dydx)2+7y=sinx
(iii) d4ydx4−sin(d3ydx3)=0
View Solutionमान लीजिए कि A=[0101] हो तो दिखाइए कि सभी n∈N के लिए (al+bA)n=anI+nan−1bA, जहाँ I कोटि 2 का तत्समक आव्यूह है ।
View Solutionहाइड्रोजनपरमाणुकेप्रथमबोरकक्षककीत्रिज्याrहै,तबLi^(2+) के प्रथम कक्षक की त्रिज्या होगी :
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=[→a.→d][→a→b→c]
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=(→a.→d)[→a→b→c]
View Solutionयदि →a,→b,→c इस प्रकार कि इकाई सदिश है कि →a.→b=0=→a.→c तथा →b और →c के मध्य का कोण π6 है , तब सिद्ध कीजिए कि →a=±2(→b×→c)
View Solutionसिद्ध कीजिए कि [ˆiˆjˆk]+[ˆiˆkˆj]=0
View Solutionसिद्ध कीजिए कि (→a×→b)×(→c×→d)=[→a→b→d]→c−[→a→b→c]→d
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि शंकु की त्रिज्या 5 से. मी. हो, तो उसका व्यास होगा
View Solution
