मान लीजिये की X का बंटन B(6,12) द्विपद बंटन है। दर्शाया कि X=3 अधिकतम प्रायिकता वाला परिणाम है।
(संकेत: P(X=3) सभी P(xi),xi=0,1,2,3,4,5,6 में से अधिकतम है।
X एक यादृच्छिक चर है जिसका द्विपद बंटन B(6,12) है।
अतः n=6 तथा p=12 तथा q=1−p=1−12=12
तब, P(X=r)=(6Cr).(12)r.(12)6−r
जहाँ
P(X=0)=(6C0).p0.q6=(6C0)(12)6=126=164
P(X=1)=(6C1).p1q5=6(12)(12)5=6(126)=664
P(X=3)=(6C2)p2q4=6×51×2.(12)2(12)4=1564
P(X=3)=(6C3)p3q3=6×5×41×2×3(12)3(12)3=2064
P(X=5)=4C5p5q1=(6C1).(12)5(12)1=664
तथा P(X=6)=(6C6)p6q0=1×(12)6=164
यह स्पर्श है कि सभी परिणामों में 2064 अधिकतम मान है। अतः X=3 अधिकतम प्रायिकता वाला परिणाम है।
Topper's Solved these Questions
- प्रायिकता BOOK - NOOTAN HINDICHAPTER - प्रायिकता EXERCISE - विविध प्रशनावली
20 Videos
- प्रायिकता BOOK - NOOTAN HINDICHAPTER - प्रायिकता EXERCISE - प्रशनावली 13.4
17 Videos
- प्रतिलोम त्रिकोणमितीय फलन BOOK - NOOTAN HINDICHAPTER - प्रतिलोम त्रिकोणमितीय फलन EXERCISE - विविध प्रश्नावली
17 Videos
- रैखिक प्रोग्रामन BOOK - NOOTAN HINDICHAPTER - रैखिक प्रोग्रामन EXERCISE - प्रश्नावली (विविध प्रश्नावली )
10 Videos
Similar Questions
A or B इस प्रकार घटनाएं है कि P(A)≠0. P(B/A) ज्ञात कीजिये यदि
(i) A, समुछ्या B का उपसमुछ्या है (ii) A∩B=ϕ
View Solutionबताइये की निम्नलिखित प्रायिकता बंटनों में कौन- से एक यादृच्छिक चर के लिए सम्भव नहीं हैं? अपना उत्तर कारण सहित लिखिए।

View Solutioncos−1(cos13π6)
View Solutionएक आहारविद दो भोज्यों P और Q का उपयोग करते हुए एक विशेष आहार तैयार करता है । भोज्य P का प्रत्येक पैकेट (जिसमे 30 ग्राम अंतव्रिष्ट है) में कैल्शियम के 6 मात्रक और विटामिन A के 6 मात्रक अंतव्रिष्ट हैं जबकि उसी मात्रक के भोज्य Q के पैकेट में कैल्शियम तत्व के 3 मात्रक, लौह-तत्व के 20 मात्रक, कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अंतव्रिष्ट हैं । आहार में कम-से कम 240 मात्रक कैल्शियम, लौह-तत्व के कम-से-कम 460 मात्रक और कोलेस्ट्रोल के अधिक-से-अधिक 300 मात्रक अपेक्षित हैं । आहार में विटामिन A के मात्रा का अधिकतमीकरण करने के लिए प्रत्येक भोज्य के कितने पैकेटों का उपयोग होना चाहिए? आहार में विटामिन A की अधिकतम मात्रा क्या है?
View Solutionएक याद्द्च्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-
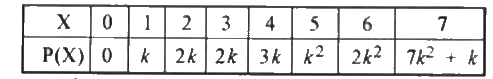 ज्ञात कीजिये-
ज्ञात कीजिये-
(i) k
(ii) P(X < 6)
(iii) P(X ge 6) (iv) P(0 < X <5)
View Solutionमान X एक याद्द्च्छिक चर है जो मान x1,x2,x3,x4 इस प्रकार ग्रहण करता है कि 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4) चर X का प्रायिकता बंटन ज्ञात कीजिए।
View Solutionनिमीनलिखित क्या X का प्रायिकता बंटन है?
 क्यों?
क्यों?
View Solutionx1+x2≤10,−2x1+3x2≤15x1≥6x1,x2≥0 से सम्बंधित उददेश्य फलन Z=x1+x2 के सुसंगत क्षेत्र का अधिकतम मान है
View Solutionमान X एक याद्द्च्छिक चर है जो मान x1,x2,x3,x4 इस प्रकार ग्रहण करता है कि 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4) चर X का प्रायिकता बंटन ज्ञात कीजिए।
View Solutionएक बहुविकल्पीय प्रश्न का उत्तर देने में विद्यार्थी या तो प्रश्न का उत्तर जानता है या जानता लगाता है | मान ले कि उसके उत्तर जान ने कि प्रायिकता 35 है तथा अनुमान लगाने कि प्रायिकता 25 है | मान ले कि छात्र के प्रश्न का उत्तर अनुमान लगाने पर सही उत्तर देने कि प्रायिकता 13 है , तो इसकी क्या प्रायिकता है कि कोई छात्र प्रश्न का उत्तर जानता है यदि यह ज्ञात है कि उसने सही उत्तर दिया है ?
View Solutionयदि (X0,Y0) समीकरणों (2x)log2=(3y)log3,3logx=2logy का हल है तो X0 का मान है
View SolutionBX3+NH3→BX3.NH3+ योगोत्पाद निर्माण की ऊष्मा (ΔH)
निम्न में से किसके लिए ΔH का संख्यात्मक मान अधिकतम पाया जाता है?
View Solutionकिस स्थिति में जल के अणुओं की संख्या अधिकतम है?
View Solutionनिम्नलिखित में से किस आयन के चुंबकीय आघूर्ण का मान अधिकतम होता है?
View Solutionबंध कोण H-X-H, किस यौगिक में अधिकतम है?
View Solution
