चित्र में दिखाये निकाय के हिस्से है : ( i ) 3R बहरी त्रिज्या की रिंग, जो क्षैतिज सतह पर ω कोणीय चाल से दक्षिणावर्त बिना फिसले लुढ़क रही है तथा (ii) 2R त्रिज्या की भरी जो ω/2 कोणीय चाल से वामावर्त घूम रही है ।।घरषरहित बॉल - बियरिंग ( गोलियां ) रिंग तथा डिस्क को एक-दूसरे से अलग रखते है। निकास X - Z - तल में है । भीतरी डिस्क पर बिंदु पर बिंदु P मूलबिंदु से र दुरी पर है, जहां OP क्षैतिज से 30∘ का कोण बनता है। तब क्षैतिज सतह के सापेक्ष:

बिंदु O का रेखीय वेग 3Rωˆi है
बिंदु P का रेखीय वेग 114Rωˆi+√34Rωˆiहै
बिंदु P का रेखीय वेग 134Rωˆi−√34Rωˆkहै
बिंदु P का रेखीय वेग (3−√34)Rωˆi+14Rωˆkहै
The correct Answer is:B
बिंदु O का रेखय वेग, v0=ω(3R)ˆi=3Rωˆi
बिंदु P पर रेखीय वेग Rω2 को X - तथा Z - अक्ष के अनुदिश वियोगित करने पर
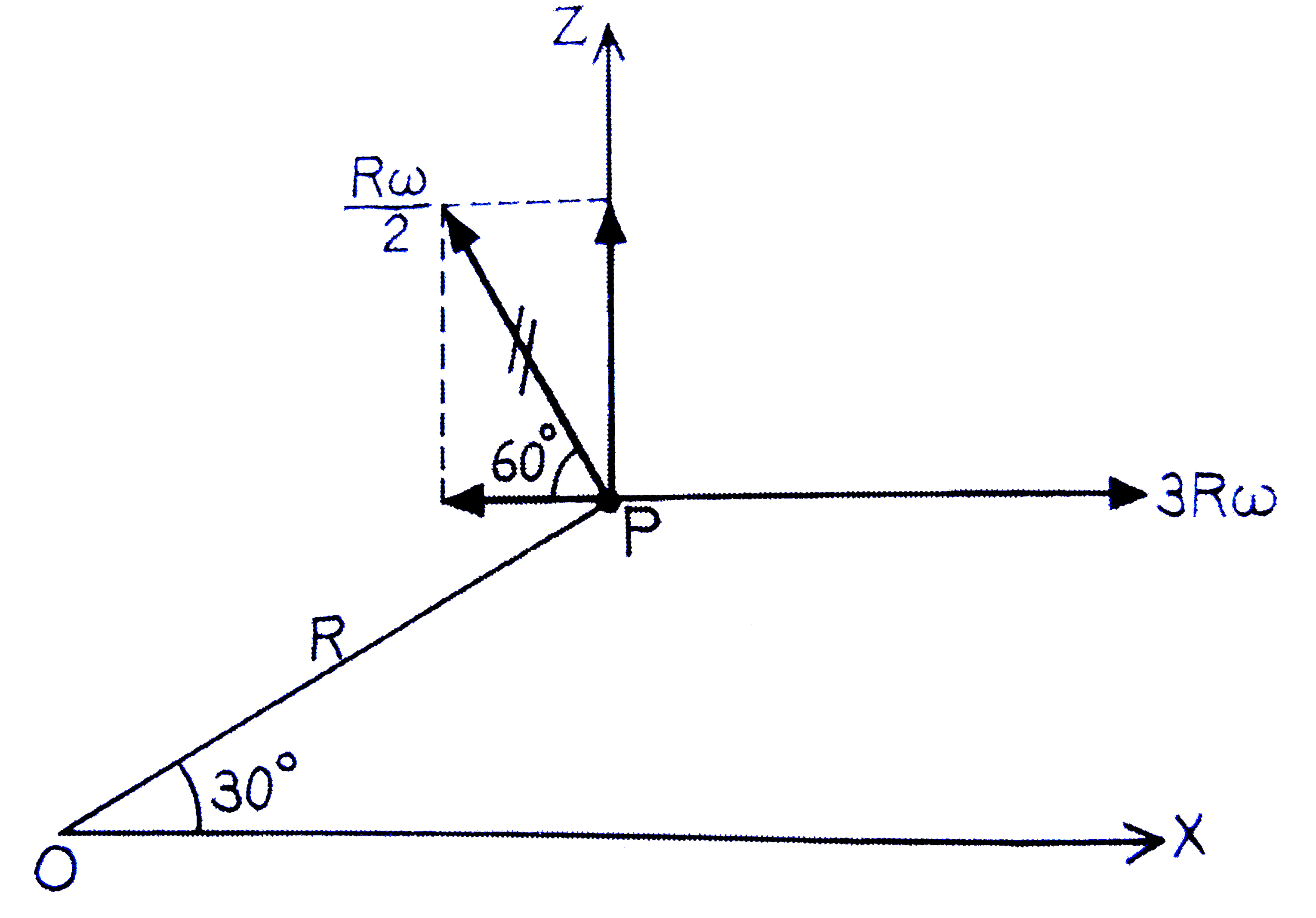
vp=3Rωˆi−Rω2cos60∘ˆi+Rω2sin60∘ˆk
=114Rωˆi+√34Rωˆk.
Topper's Solved these Questions
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - एन सी ई आर टी प्रशन
23 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - आंकिक
40 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिरिक्त प्रश्न
9 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिरिक्त प्रश्न
7 Videos
Similar Questions
निम्नलिखित पर कार्यत नेट बल का पैमान व् उसकी दिशा लिखिय :
(a) एक समान चाल से निचे गरती वर्षा की कोई बून्द,
(b) जल में तैरता 10 g शांति का कोई कार्क,
(c) कुशलता से आकाश में स्थिर रोकी गई कोई पंतंग,
(d) 30 h−1 के एकसमान वेग से उबड़ - खावड़ सड़क पर गतिशील कोई कार,
(e) सभी गुरुत्वीय पिंडो से दूर तथा विधुत और चुम्बकीय क्षेत्रों से मुक्त, अंतरिक्ष में तीव्र चाल वाला इलेक्ट्रॉन ।
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View Solutionएक व्रत पर गति करते कण का वेग 5 मीटर/सेकंड तथा आम्लम्ब त्वरण 10 मीटर/सेकण्ड2 है । व्रत की त्रिज्या ज्ञात कीजिय |
View Solutionवर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके उर्ध्व के साथ θ कोण बनाना पड़ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युतपन्न करता है :
tanθ=v,
और वह इस संबंध के औचित्य की सिमा पता लगाता है, जैसी की आशा की जाती है यदि v → 0 तो θ→0 | (हम यह मान रहे हैं की तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा उर्ध्वाधरत: पद रही है) । क्या आप सोचते हैं की यह संबंध सही हो सकता है ? यदि ऐसा नहीं है तो सही संबंध का अनुमान लगाइए ।
View Solutionकिसी सदिश में परिमाण व् दिशा दोनों होते है | क्या दीकस्थान में इसकी कोई स्थिति होती है ? क्या यह समय के साथ परिवर्तित हो सकता है | क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों →a व →b का समान भौतिक प्रभाव अवश्य पड़ेगा ? अपने उत्तर के समर्थन में उदाहरण दीजिए |
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View Solutionउस वृत्त का समीकरण जिसका केन्द्र x-अक्ष पर है तथा त्रिज्या 4 है। और जो मूल बिन्दु से होकर जाता है, होगा
View SolutionEquation of the circle whose center x-अक्ष पर है तथा त्रिज्या 4 है। और जो मूल बिन्दु से होकर जाता है, होगा
View Solutionजो चीजों से उठती अंधेपन की भाप पर दुलक जाती है' में कौन-सा अलंकार है ?
View Solutionअलग-अलग जगहों पर खड़िया-पट्टी के अलग-अलग नामों में से एक है
View Solution
