R त्रिज्या का पतला वृतीय तार अपने ऊर्ध्वाधर व्यास के पृथ कोणीय आवृति ω से घर्षण कर रहा है । यह दर्शाइए की इस तार में डली कोई मनिका ω≤√g/R के लिए अपने निम्नतम बिंदु पर रहती है । ω=√2g/R के लिए, केंद्र से मनिका को जोड़ने वाला त्रिज्या सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कौन बनता है ? ( घर्षण को अपेक्सनीय मनीय ।)
माना R त्रिज्या का पतला वृतिया तार ( जैसा की त्रिज्या में प्रदर्शिक्त है ) अपने ऊर्ध्वाधर व्यास AB के परितः ω कोणीय वेग से घर्षण कर रहा है । माना किसी क्षण, m द्रव्यमान की एक मनिका वृतीय तार की भीतरी सतह के बिंदु P पर इस प्रकार स्थित है की मनिका P को वृतीय तार के केंदरत O को मिलाने वाली रेखा OP जिसे त्रिज्या सदिश भी कह सकते है ऊर्ध्वाधर व्यास AB से निचे की और θ कौन बनाती है ( चित्र देखें ) । मनिका पर कार्यरत बालो पर विचार करने पर, (i) मनिका का भर mg जो की ऊर्ध्वाधर निचे को व्यास AB के समांतर दृष्टि है ।
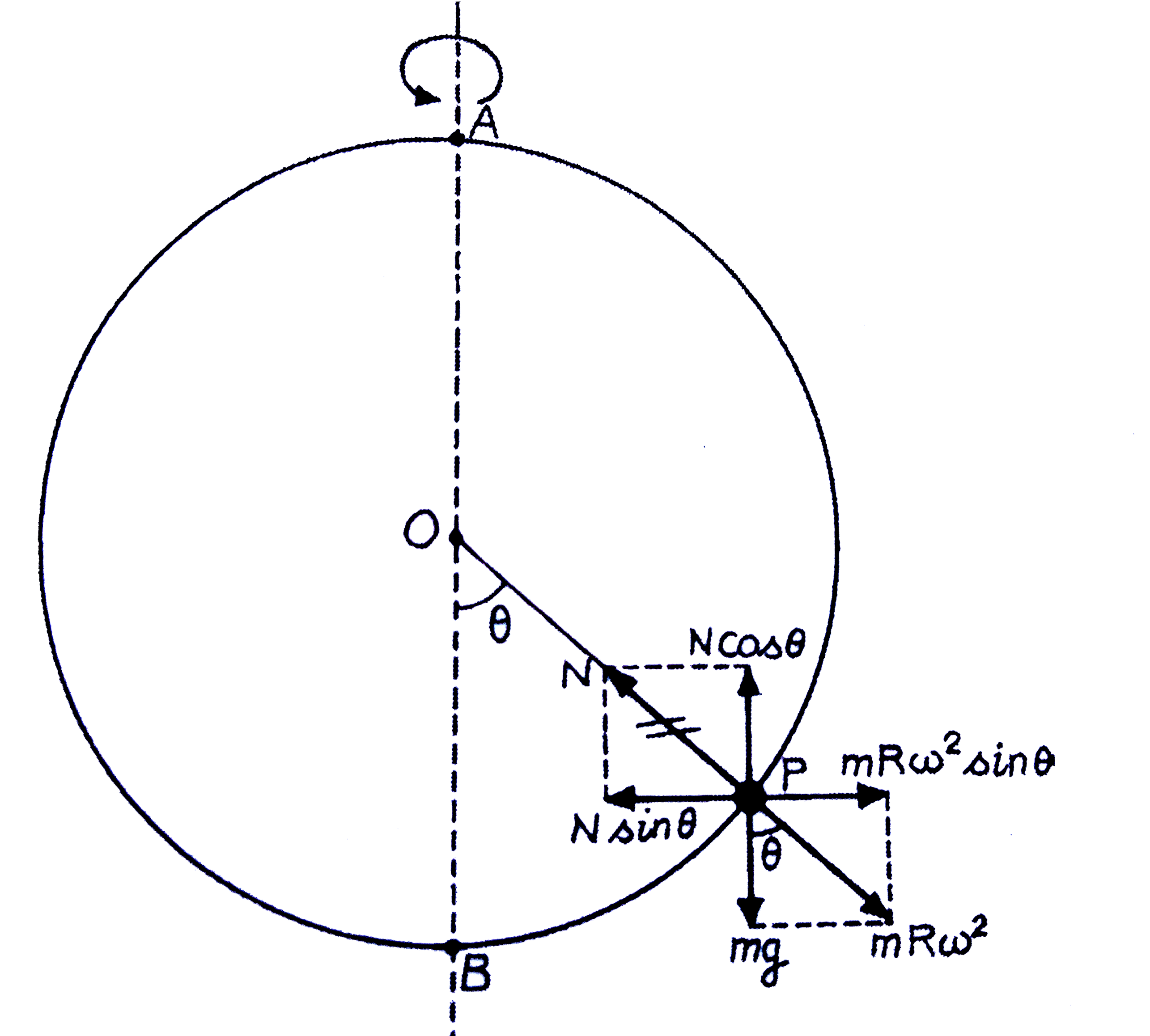
(ii) Nsinθ=mRω2sinθअथवा N=mRω2 ...(i)
मनिका पर वृतीय तार के ताल की अभिलम्ब प्रतिक्रिया N, त्रिज्या सदिश के अनुदिश केन्देर की और निर्दिष्ट है ।
(iii) वृतीय गति के लिए आवशयक अभिकेंडर - बल mRω2 जो त्रिज्या सदिश के अनुदिश ही कार्यरत है ।
माणिक के संतुलन के लिए,
तथा Ncosθ=mg
समीकरण (i) व् (ii) से,
cosθ=mgN=mgmRω2=gRω2
अथवा ω=√gRcosθ ...(iii)
चूँकि θ के निश्चित मान के लिए ।cosθ।≤1।
अतः यदि ω≤√gR, तो मनिका निम्नतम बिंदु पर रहती है ।
पुनः समाकरण (iii) में ω=√2gR प्रतिस्थापित करने पर,
√2gR=√2gRcosθ
cosθ=12
अथवा θ=cos−1(12)=60∘.
Topper's Solved these Questions
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - एन सी ई आर टी प्रशन
23 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिरिक्त प्रश्न
9 Videos
- सदिश विश्लेषण एवं प्रक्षेप्य गति BOOK - NOOTAN HINDICHAPTER - सदिश विश्लेषण एवं प्रक्षेप्य गति EXERCISE - अतिरिक्त प्रश्न
7 Videos
Similar Questions
निम्नलिखित पर कार्यत नेट बल का पैमान व् उसकी दिशा लिखिय :
(a) एक समान चाल से निचे गरती वर्षा की कोई बून्द,
(b) जल में तैरता 10 g शांति का कोई कार्क,
(c) कुशलता से आकाश में स्थिर रोकी गई कोई पंतंग,
(d) 30 h−1 के एकसमान वेग से उबड़ - खावड़ सड़क पर गतिशील कोई कार,
(e) सभी गुरुत्वीय पिंडो से दूर तथा विधुत और चुम्बकीय क्षेत्रों से मुक्त, अंतरिक्ष में तीव्र चाल वाला इलेक्ट्रॉन ।
View Solutionवर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके उर्ध्व के साथ θ कोण बनाना पड़ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युतपन्न करता है :
tanθ=v,
और वह इस संबंध के औचित्य की सिमा पता लगाता है, जैसी की आशा की जाती है यदि v → 0 तो θ→0 | (हम यह मान रहे हैं की तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा उर्ध्वाधरत: पद रही है) । क्या आप सोचते हैं की यह संबंध सही हो सकता है ? यदि ऐसा नहीं है तो सही संबंध का अनुमान लगाइए ।
View Solutionकिसी सदिश में परिमाण व् दिशा दोनों होते है | क्या दीकस्थान में इसकी कोई स्थिति होती है ? क्या यह समय के साथ परिवर्तित हो सकता है | क्या दिक्स्थान में भिन्न स्थानों पर दो बराबर सदिशों →a व →b का समान भौतिक प्रभाव अवश्य पड़ेगा ? अपने उत्तर के समर्थन में उदाहरण दीजिए |
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionनिम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए
शांभा- "हमारे प्यारे सरपंच के हुकम से इस कंजूस किरोड़ीमल को सजा दी जाती है कि यह उसी लड़की से जाकर अपने लड़के की शादी कम व्यय में करे। अपने समधी से माफी माँगे।
किरोड़ीमल को सजा कौन देता है ?
View Solutionनिम्नलिखित मै से कोई एक गद्यांश को पढ़कर उसके निचे दिए गये प्रश्न के उतर लिखिए शांभा- "हमारे प्यारे सरपंच के हुकम से इस कंजूस किरोड़ीमल को सजा दी जाती है कि यह उसी लड़की से जाकर अपने लड़के की शादी कम व्यय में करे। अपने समधी से माफी माँगे। किरोड़ीमल को किससे क्षमा माँगने के लिए कहा गया है ?
View Solutionनिम्नलिखित व्यंजकों में से कौन-कौन से बहुपद है | अपने उत्तर के लिए कारण लिखिए :
3√x+x2
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View SolutionA solid sphere of brass with a radius 15 cm is drawn into a wire of diameter 6 mm. The length of the wire ( in cm ) is :
15 cm त्रिज्या वाले पीतल के एक ठोस गोले को 6 mm व्यास के तार में खिंचा जाता है | तार की लम्बाई (cm में) है:
View SolutionM, N, P, R, T, W, F and H are sitting around a circle at the centre, P is third to the left of M and second to the right of T. N is second to the right of P. R is second to the right of W who is second to the right of M. F is not an immediate neighbour of P. Who is to the immediate right of P?
M, N, P, R, T, W, F और H केंद्र में एक वृत्त के चारों ओर बैठे हैं,P, M के बाएं से तीसरे और T के दायें से दूसरे स्थान पर हैं| N, Pके दाईंओर दूसरा है। R, W के दायें से दूसरे नंबर पर है, जो M के दायें से दूसरे नंबर पर है, P का तत्काल पड़ोसी नहीं है। P के तत्काल दाएं को कौन है?
View SolutionIf '+' stands for'+', '-' stands for '=', 'x' stands for '+', '+' stands for greater than, '=' stands for less then, '>' stands for multiplication and '<' stands for subtraction, then which of the following alternatives is correct?
View Solutionनिम्नलिखित में से कौन सा, 2s कक्षक के लिए इलेक्ट्रॉन के पाये जाने की अरीय प्रायिकता का सही मिलान है
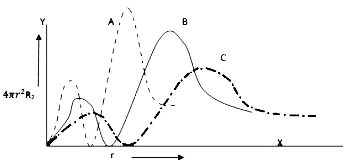
View Solutionएक एंजाइम उत्प्रेरित अभिक्रिया के लिए, ताप (T) के सापेक्ष अभिक्रिया की दर (r) को आलेखित किया गया है। निम्नलिखित में से कौन सा सही निरूपण है?
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solutionआयनिक त्रिज्या के निम्नलिखित क्रम में से कौन सा सही ढंग से प्रदर्शित किया गया है?
View Solutionनिम्नलिखित में से कौन सी नाम अभिक्रिया एक -COOH समूह को निरूपित करने के लिए उपयोग नहीं की जाती है?
View Solution
