Find the values of m for which roots of equation x2−mx+1=0 are less than unity.
Let f(X)=x2−mx+1 as both roots of f(x)=0 are less than 1 we can take D≥0,af(1)≥0 and −b2a<1
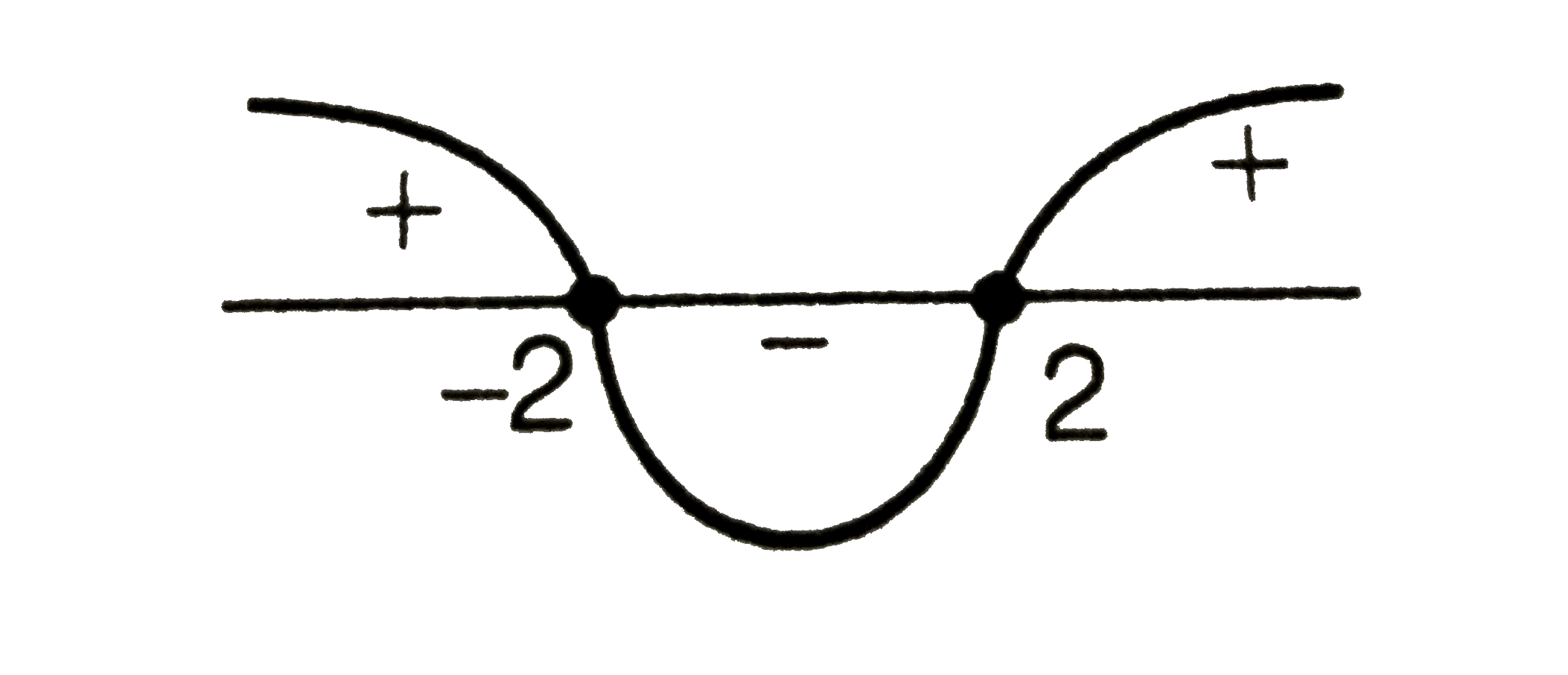 ltBrgt (i) Consider D≥0(−m)2−4.1.4≥0
ltBrgt (i) Consider D≥0(−m)2−4.1.4≥0
⇒(m+2)(m−2)≥0
⇒mε(−∞,−2[∪[2,∞)…......i
(ii) Consider af (1)>01(1−m+1)>0
⇒m−2<0⇒m<2
⇒mε(−∞,2) .......ii
(iii) Consider (−b2a<1)
m2<1⇒m<2
⇒mε(−∞,2)........iii
Hence the values of m satisfying Eqs. (i), (ii) and (iii) at the same time are mε(−∞,−2]
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 111videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 210videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)44videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
The set of all values of a for which both roots of equation x2−ax+1=0 are less than unity is (A) (−∞,−2) (B) (−2,∞) (C) (−2,3) (D) (−∞,−1)
View SolutionThe set of all value of a for which one root of equation x2−ax+1=0 is less than unity and other greater than unity (A) (−∞,2) (B) (2,∞) (C) (1,∞) (D) none of these
View Solution
Knowledge Check
- Question 1 - Select One
Find the valuesof m for which exactly one root of the equation x2−2mx+m2−1=0 lies in the interval (−2,4)
Am>3B−1<m<3C1<m<4D−2<m<4
Find the set of all values of a for which the roots of the equation x2−2ax+a2+a−3=0 are less than 3,
View SolutionFind the values of a for which one root of equation (a−5)x2−2ax+a−4=0 is smaller than 1 and the other greater than 2.
View SolutionConsider the quadratic equationx2−mx+1=0 with two roots αand β such that α+β=m and αβ=1 The value of m for which both the roots of the equation are less than unity are (A) ]−∞,−2] (B) [−2,2] (C) [2,∞] (D) ]−∞,−2]∪[2,∞]
View SolutionFind the valuesof m for which exactly one root of the equation x2−2mx+m2−1=0 lies in the interval (−2,4)
View SolutionAll the values of m for whilch both the roots of the equation x2−2mx+m2−1=0 are greater than -2 but less than 4 lie in the interval
A −2<m<0
B. m>3
C. −1<m<3
D. 1<m<4View SolutionConsider the quadratic equationx2−mx+1=0 with two roots αand β such that α+β=m and αβ=1 The value of m for which both the roots of the equation are greater then unity re (A) [2,∞] (B) ]−−∞,2] (C) [−2,2] (D) none of these
View SolutionThe value of k for which both the roots of the equation 4x2−20kx+(25k2+15k−66)=0 are less than 2, lies in
View Solution

