Doubtnut Promotions Sticky

Solv ethe equation |x−1|+|7−x|+2|x−2|=4

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Here critical points are 1,2,7 using the method of intervals, we find intervals when the expression x−1,7−x and x−2 are of constant signs.
i.e. x<1,1<x<2,2<x<7,x>7
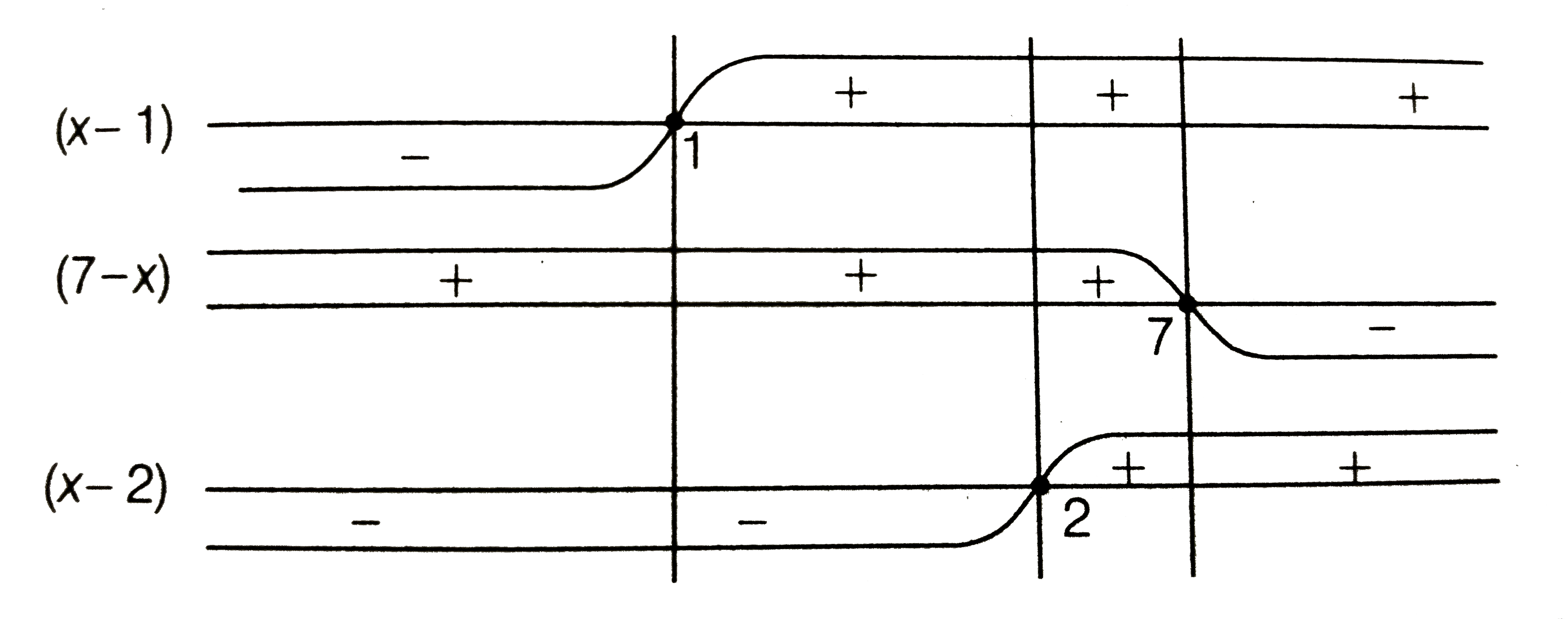
ocr_image
Thus, the given equation is equivalent to the collection of four systems,
⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣{x<1−(x−1)+(7−x)−2(x−2)=4{1≤x<2(x−1)+(7−x)−2(x−2)=4{2≤x<7(x−1)+(7−x)+2(x−2)=4{x≥7(x−1)−(7−x)+2(x−2)=4implies[({(xlt1),(x=2):}),({(1lexlt2),(x=3):}),({(2lexlt7),(x=1):}),({(xge7),(x=4):}):}
From the collection of four systems, the given equation has no solution.

|