If α,β be the roots of 4x8−16x+c=0,c∈R such that 1<α<2and2<β<3, then the number of integral values of c is
Video Solution
Text Solution
The correct Answer is:3
∵4x2−16x+c=0
⇒x2−4x+c4=0
Let f(x)=x2−4x+c4
Then the following case arises:
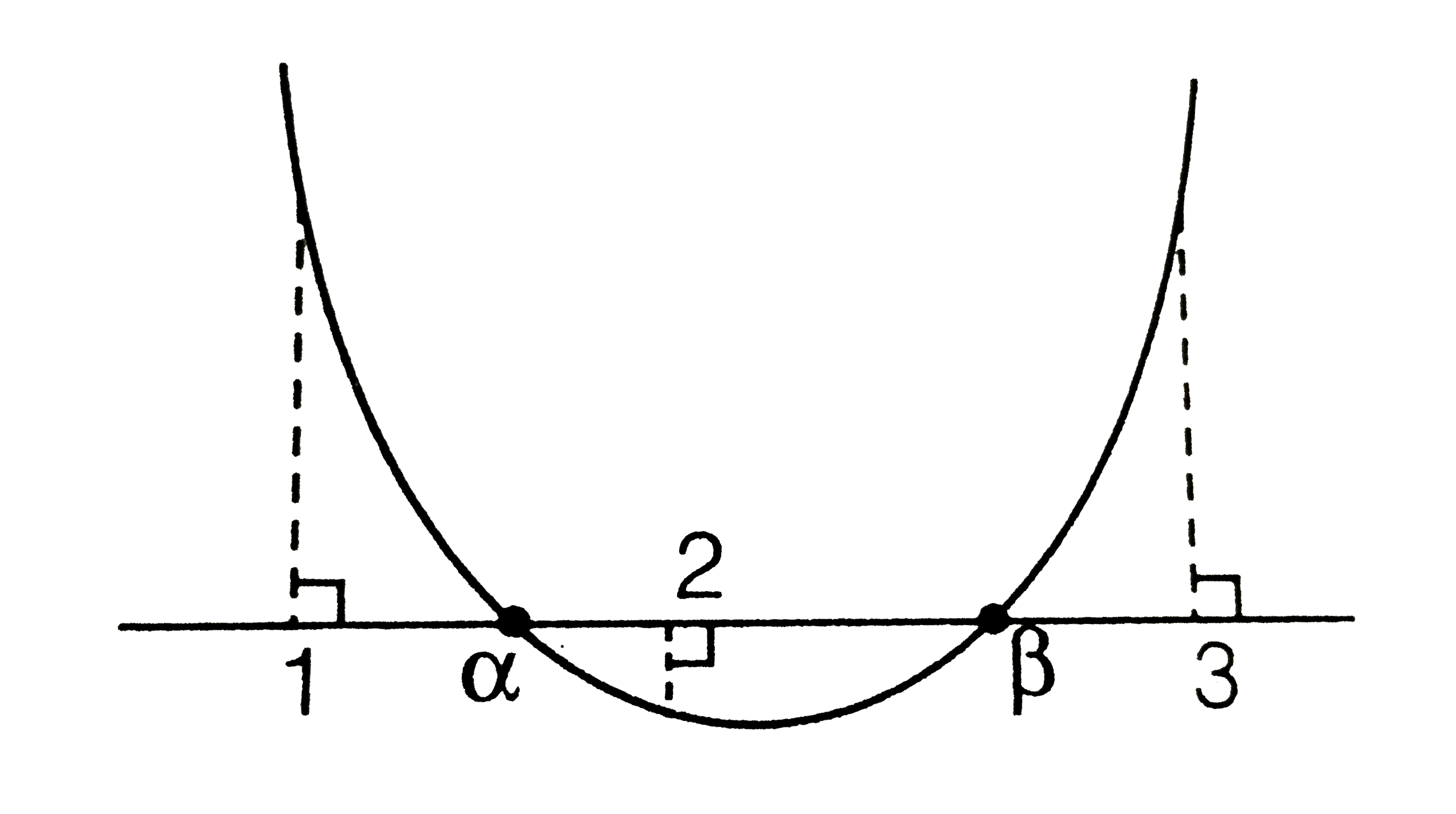
Case I D>0
=16−c>0
∴c<16
Case II f(1)>0 ltbr ⇒1−4+c4>0
⇒c4>3
∴c>12
Case III f(2)<0
⇒4−8+c4<0
⇒c4<4
c<16
Case IV f(3)>0
⇒9−12+c4>0
⇒c4>3
⇒c>12
Combining all cases, we get
12<c<16
Thus, integral values of c are 13, 14 and 15.
Hence number of integral values of c is 3.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matching Type Questions)2videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - MATCH TYPE2videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Passage Based Questions)21videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)44videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
If α,β be the roots of 4x2−16x+c=0,c∈R such that 1<α<2and2<β<3, then the number of integral values of c is
A5B6C2D3 - Question 2 - Select One
If αandβ are the roots of the equation x2+αx+β=0 such that α≠β, then the number of integral values of x satisfying ||x−β|−α|<1 is
A0B1C2Dmore than 2 - Question 3 - Select One
If αandβ(α<β) are the roots of the equation x2+bx+c=0, where c<0<b, then
A0<α<βBα<0β<|α|Cα<β<0Dα<0<|α|<β
"If α~β be the roots of the equation 4x2−16x+λ=0 where λ∈R such that 1<α<2 and 2<β<3 then number of integral values of λ is A. 5 B. 6 C. 2 D. 3
View SolutionIf α,β are the roots of x2−3x+a=0,a∈Rand<1<β,
then find the values of aView SolutionConsider the triangle pictured as shown. If 0<α<π2 then the number of integral values of c is
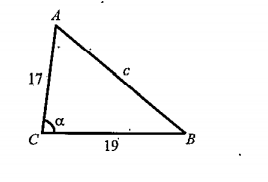 View Solution
View SolutionIf the equation ax2+bx+c=0(a<0) has two roots α and β such that α<−3 and β>3, then
View SolutionIf α,β are the roots of the equation 2x2+6x+b=0,(b<0) then αβ+βα is less than
View Solution

