for what values of m, the equation 2x2,−2(2m+1),x+m(m+1)=0m∈R has
(i) Both roots smallar than 2 ?
(ii) Both roots greater than 2 ?
(iii) Both roots lie in the interval (2,3) ?
(iv) Exactly one root lie in the interval (2,3) ?
(v) One root is smaller than 1, and the other root is greater than 1 ?
(vi) One root is greater than 3 and the other root is smaller than 2 ?
(vii) Roots αandβ are such that both 2 and 3 lie between αandβ ?
The correct Answer is:(i) mεg(−∞,7−√32) (ii) mε(7+√332,∞) (iii) mεϕ
(iv) mε(7−√32,11−√732)∪(7+√332,11+√732)
(v) mε(0,3) (vi) mε(7−√32,7+√332)
(vii) mε(7−√332,11−√732)∪(7+√332,11+√732)
(viii) mε(7−√32,7+√332)∪(7+√32,∞)
(ix) mε(−∞,7−√332)∪((7−√332,7+√332)
(x) mε((11-sqrt(73))/2,(7+sqrt(3))/2)
∵2x2−2(2m+1)x+m(m+1)=0[∵mεR]
∴D=[−2(2m+1)]2−8m(m+1)[D=b2−4ac]
=4{(2m+1)2−2m(m+1)}
=4(2m2+2m+1)
=8(m2+m+12)=8{(m+12)2+14}>0
or D>0,∀mεolonR……i
x coordinate of vertex =−b2a=2(m+1)4=(m+12).....ii
and let
f(x)=x2−(2m+1)x+12m(m+1) ...........iii
(i) Both roots are smaller than 2.

Consider the following cases:
Case I D≥0
∴mεR [from Eq. (i) ]
CaseII x-coordinate of vertex <2.
⇒m+12<0 [from Eq. (ii) ]
or m<32
Case III f(2)>0
⇒4−(2m+1)2+12m(m+1)>0
⇒m2−7m+4>0
∴mε(−∞,7−√32)∪(7+√332,∞)
Combining all cases we get
mε(−∞,7−√32)
(ii) Both roots are greater than 2.
Consider the following cases.
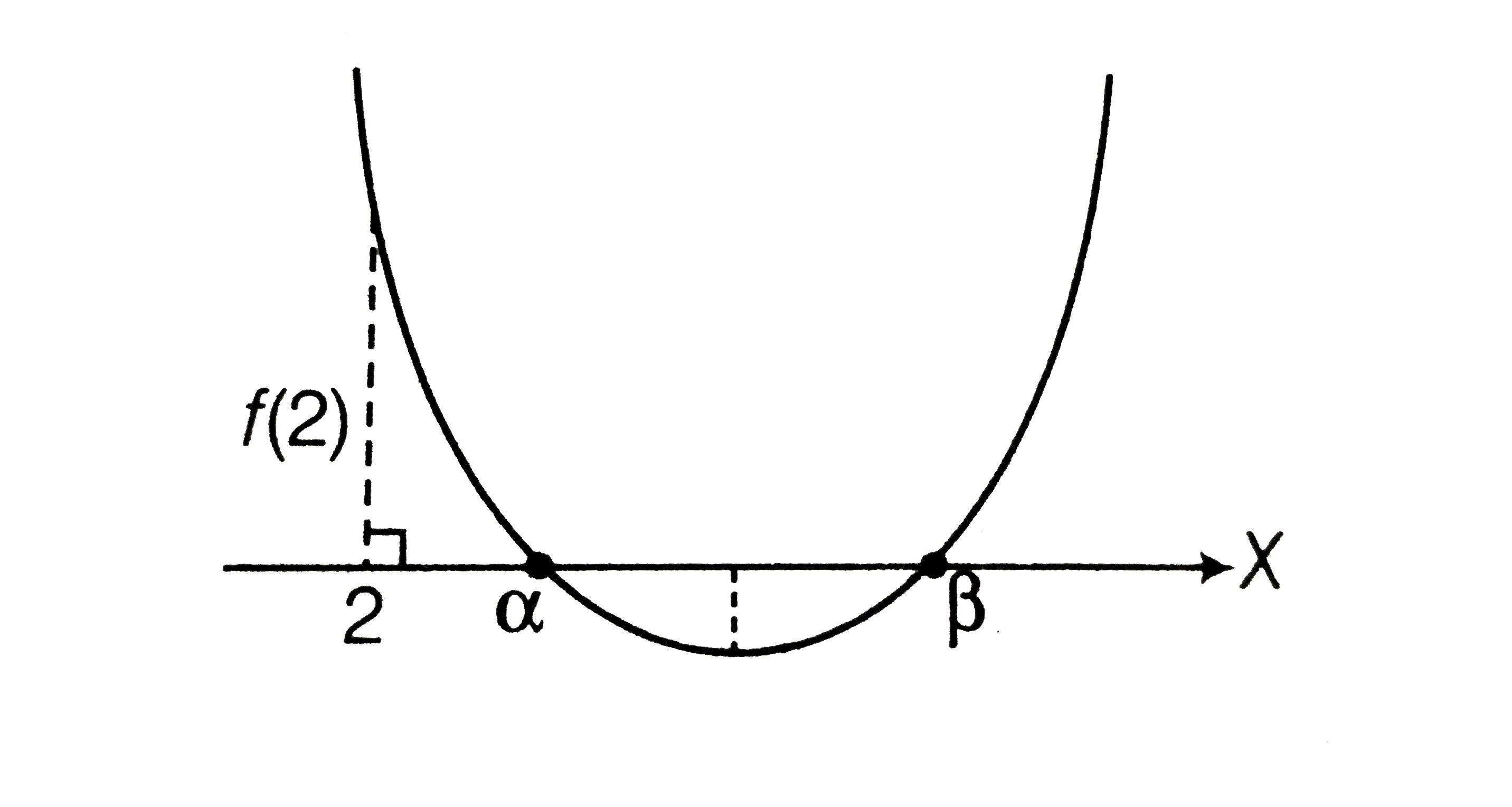
Case I D≥0
∴mεR[from Eq. (i)]
Case II x- coordinate of vertex >2
⇒m+12>2[ from Eq. (ii)]
∴m>32
Case III f(2)>0
mε(−∞,7−√332)∪(7+√332,∞) [from part (a) ]
Combining all cases, we get
mε(7+√332,∞)
(iii) Both roots lie in the interval (2,3).
Consider the following cases:

CAse I D≥0
∴mεR [from Eq. (i)]
Case II f(2)>0
∴mε(−∞,7−√32)∪(7+√332,∞) [from part (a)]
Case Case III f(3)>0
⇒9−3(2m+1)+12m(m+1)>0
or m2−11m+12>0
:mε(−∞,11−√732)∪(11+√732,∞)
Case IV 2<x -coordinate of vertex <3
⇒2<m+12<3
or 32<m<52 or mε(32,52)
Combining allcases we get
mεϕ
(iv) Exactly one root lie in the interval (2,3).
Consiser the following cases:
Case I D>0
∴mεR [from Eq (i) ]
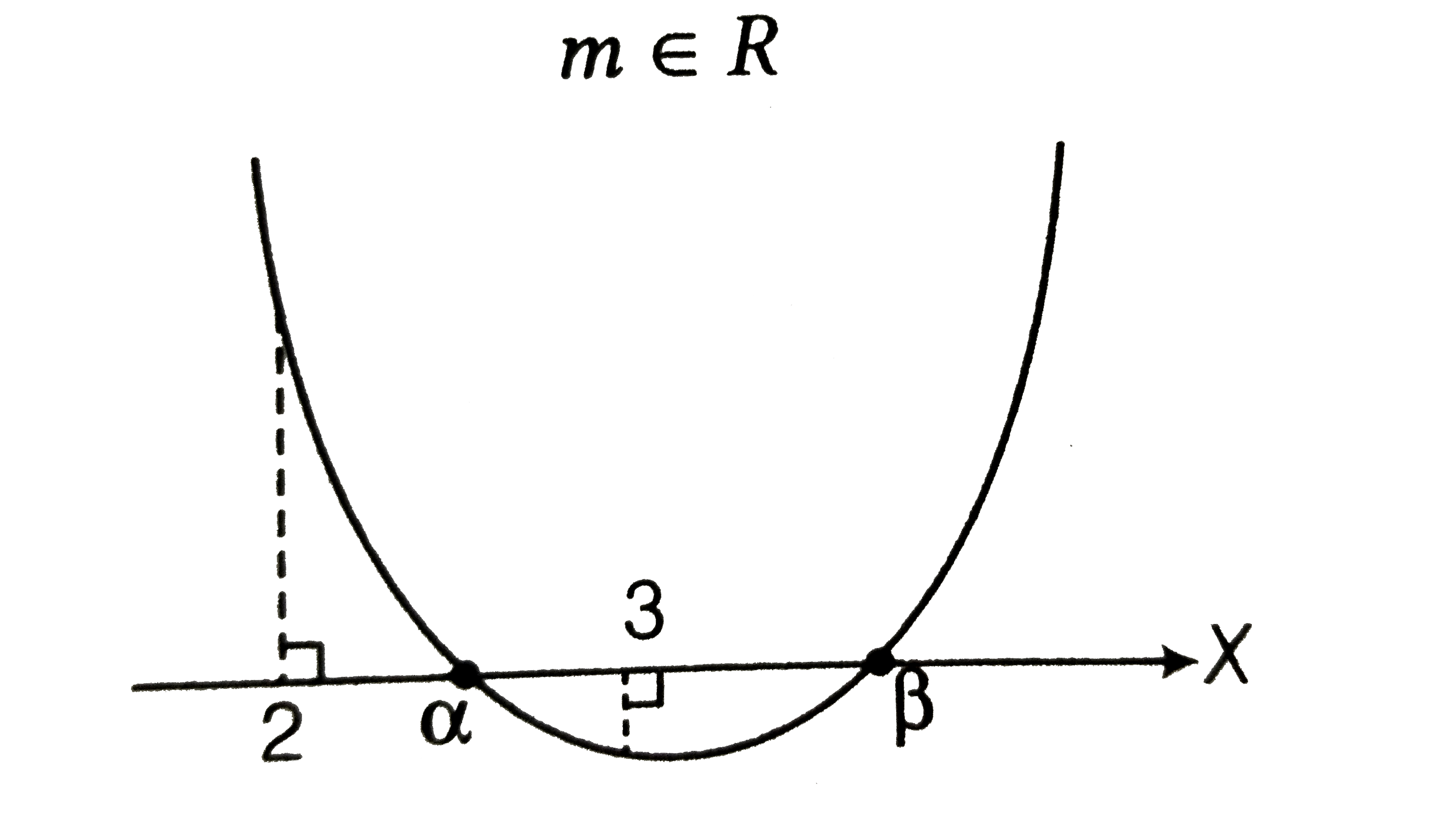
Case II f(2)f(3)<0
(4−2(2m+1)+12m(m+1))
(9−3(2m+1)+12m(m+1))<0
⇒(m2−7m+4)(m2−11m+12)<0
⇒(m−7−√332)(m−7+√332)
(m−11−√732)(m−11+√732)<0
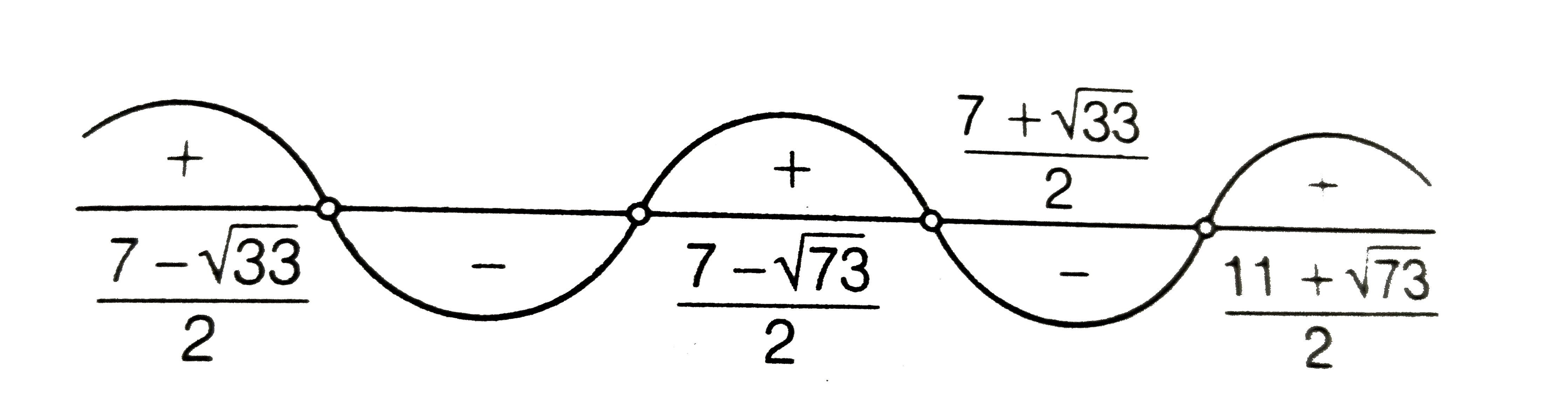
∴mε(7−√332,11−√332)∪(7+√332,11+√732)
Combining all cases we get
mε((7-sqrt(33))/2,(11-sqrt(73))/2))uu((7+sqrt(33))/2,(11+sqrt(73))/2)<br>(v)O≠i√ssmal≤rthan1andtheotheri√sgreaterthan1.<br>Consiserthefollow∈gcases.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S06.pngwh=80%mx-autosty≤=background:white;><br>CaseIDgt0<br>:.m epsilonR[omEq.(i)]<br>CaseIIf(1)lt0<br>implies1-(2+1)+1/2m(m+1)lt0[omEq.(iii)]<br>impliesm^(2)-3mlt0<br>impliesm(m-3)lt0<br>:.m epsilon (0,3)<br>Comb∈∈g⊥hcaseswe≥t<br> m epsilon(0,3)<br>(vi)O≠i√sgreaterthan3andtheotheri√ssmal≤rthan2.<bR>Consiserthefollow∈gcases<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S07.pngwh=80%mx-autosty≤=background:white;><br>CaseIDgt0<br>:. m epsion R[omEq.(i)]<br>CaseIIf(2)lt0<br>impliesm^(2)-8m+4lt0<br>:.(7-sqrt(33))/2ltmlt(7+sqrt(33))/2<br>:. m epsilon ((7-sqrt(33))/2ltm lt (7+sqrt(33))/2<br>:. M epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>CaseIIIf(3)lt0<br>impliesm^(2)-11m+12lt0<br>:.(11-sqrt(73))/2ltmlt (11+sqrt(73))/2<br>:. m epsilon ((11-sqrt(73))/2, (11+sqrt(73))/2)<br>Comb∈∈gallcaseswe≥t<br>m epsilon ((7-sqrt(33))/2, (7+sqrt(33))/2)<br>(vii)At≤∗o≠l√ies∈the∫erval(2,3).<br>i.e.(d)uu(c)<br>:.mepsilon((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)<br>(viii)At≤∗o≠i√sgreaterthan2.<br>i.e(Exactlyo≠i√sgreaterthan2)uu(Boths√aregreater2).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S08.pngwh=80%mx-autosty≤=background:white;><br>of(Exactlyo≠i√sgreaterthan2)uu(b)…..i<br>Consrthefollow∈gcases:<br>CaseIDgt0<br>:. m epsilon[omEq.(i)]<br>CaseIIf(2)lt0<br>impliesm^(2)-7m+4lt0<br>:.m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>Comb∈∈g⊥hcaseswe≥t<br>m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)………ii<br>F∈allyomEqsiandiiwe≥t<br> m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)uu((7+sqrt(33))/2,oo)<br>(ix)At≤∗o≠i√ssmal≤rthan2.<br>i.e(Exactlyo≠i√ssmal≤rthen2)uu(Boths√aresmal≤rthan2)<br>or(h)IIuu(a)<br>We≥tm epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33))/2,(7+sqrt(33))/2)<br>(x)Both2and3liebetweenalphaandbeta<br>Consrthefollow∈gcases:<br>CaseDgt0<br>:. mepsilonR[omEq(i)]<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S09.pngwh=80%mx-autosty≤=background:white;><br>CaseIIf(2)lt0<br>impliesm^(2)-7m+4lt0<br>:. m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>CaseIIIf(3)lt0<br>impliesm^(2)-11m+12lt0<br>:.m epsilon((11-sqrt(73))/2,(11+sqrt(73))/2)<br>Comb∈∈gallcaseswe≥t<br>m epsilon ((11-sqrt(73))/2,(7+sqrt(33))/2)
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)35videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Statement I And Ii Type Questions)7videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)44videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
For what values of m the equation (1+m)x2−2(1+3m)x+(1+8m)=0 has equal roots.
View SolutionDifferent condition for location of roots(vi) If α<k<β (vii)Exactly one root lying in the interval (k1,k2) (viii) Both the roots lying in the interval (k1,k2) (ix)One root is smaller than k1 and other roots is greater than k2
View Solution
Knowledge Check
- Question 1 - Select One
If the equation x2−(2+m)x+(m2−4m+4)=0 has coincident roots, then
Am=0,m=1Bm=0,m=2Cm=23,m=6Dm=23,m=1 - Question 2 - Select One
If m∈Z and the equation mx2+(2m−1)x+(m−2)=0 has rational roots, then m is of the form
An(n+2),n∈ZBn(n+1),n∈ZCn(n−2),n∈ZDnone of these
For what values of m will the equation x2−2x(1+3m)+7(3+2m)=0 have equal roots?
View SolutionLet x2−2(a−1)x+a−1=0(a∈R) be a quadratic equation, then find the values of "a" for which
(i) Exactly one root lies in (0,1)View SolutionFor what values of m does the equation, mx2+(3x−1)m+2x+5=0 have equal roots of opposite sign ?
View SolutionFind the values of the parameter a for which the roots of the quadratic equation x2+2(a−1)x+a+5=0 are
such that one root is greater than 3 and the other root is smaller than 1.View SolutionFor what value of m will the equation x2+mx−(m2+3m−32)=0 have equal roots ?
View SolutionIf the equation (1+m)x2−2(1+3m)x+(1+8m)=0, where m∈R~{−1}, has at least one root is
View Solution

