There are three teams x,x+1 and y childrens and total number of childrens in the teams is 24. if two childrens of the same team do not fight, then
maximum number of fights is 190
maximum number of fights is 191
maximum number of fights occur when x=7
maximum number of fights occur when x=8
The correct Answer is:B, C, D
∵x+x+1+y=24
⇒y=23−2x
Let N=Total number of fights subject to the condition that any two children of one tem do not fight.
∴N=2.24C2−(.xC2+.x+1C2+.yC2)
=.24C2−(.xC2+.x+1C2+.23−2xC2)
=23−3x2+45x
∴dNdx=0−6x+45
for maximum or minimum, put dNdx=0impliex=7.5
⇒x=7 [∵x∈I]
Now, d2Ndx2<0
∴ N will be maximum when x=7
and N=23-3(7)2+45×7=191
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Passage Based Questions)
15 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Single Integer Answer Type Questions)
10 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHSCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Single Option Correct Type Questions)
30 Videos
- PARABOLABOOK - ARIHANT MATHSCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
36 Videos
- PROBABILITYBOOK - ARIHANT MATHSCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
55 Videos
Similar Questions

What is the total number of children liking CSK ?
View SolutionMr. john has x children by his first wife and Ms. Bashu has x+1 children by her first husband. They marry and have children of their own. The whole family has 10 children. Assuming that two children of the same parents do not fight, Find the maximum number of fight that can take place among children.
View Solution
Knowledge Check
Mr. A has x children by his first wife and Ms. B has x+1 children by her first husband. They marry and have children of their own. The whole family has 10 children. Assuming that two children of the same parents do not flight. The number of maximum fights that can take place______________.
A33B22C111Dnone of theseMr. john has x children by his first wife and Ms. Bashu has x+1 children by her first husband. They marry and have children of their own. The whole family has 10 children. Assuming that two children of the same parents do not fight, Find the maximum number of fight that can take place among children.
A33B22C111Dnone of these
Mr. A has x children by his first wife and Ms. B has x+1 children by her first husband. They marry and have children of their own. The whole family has 10 children. Assuming that two children of the same parents do not flight. The number of maximum fights that can take place______________.
View SolutionSohan has x children by his first wife. Geeta has (x+1) children by her first husband. The marry and have children of their own. The whole family has 24 children. Assuming that two children of the same parents do not fight, prove that the maximum possible number of fights that can take place is 191.
View SolutionJohn has x children by his first wife. Mary has (x+1) children by her first husband. They marry and have children of their own. The whole family has 24 children. Assuming that two children of the same parents do not fight prove that the maximum possible number of fights that can take place is 191.
View SolutionThere are n identical toys and n children. The number of ways of distributing the toys to the children so that exactly two of them do not get any toy is
View SolutionThe numbers of children in five families are 0, 2, 1, 3, and 4. Find the average number of children. If two families having 6 and 5 children respectively are included in it, then what is the new mean?
View Solution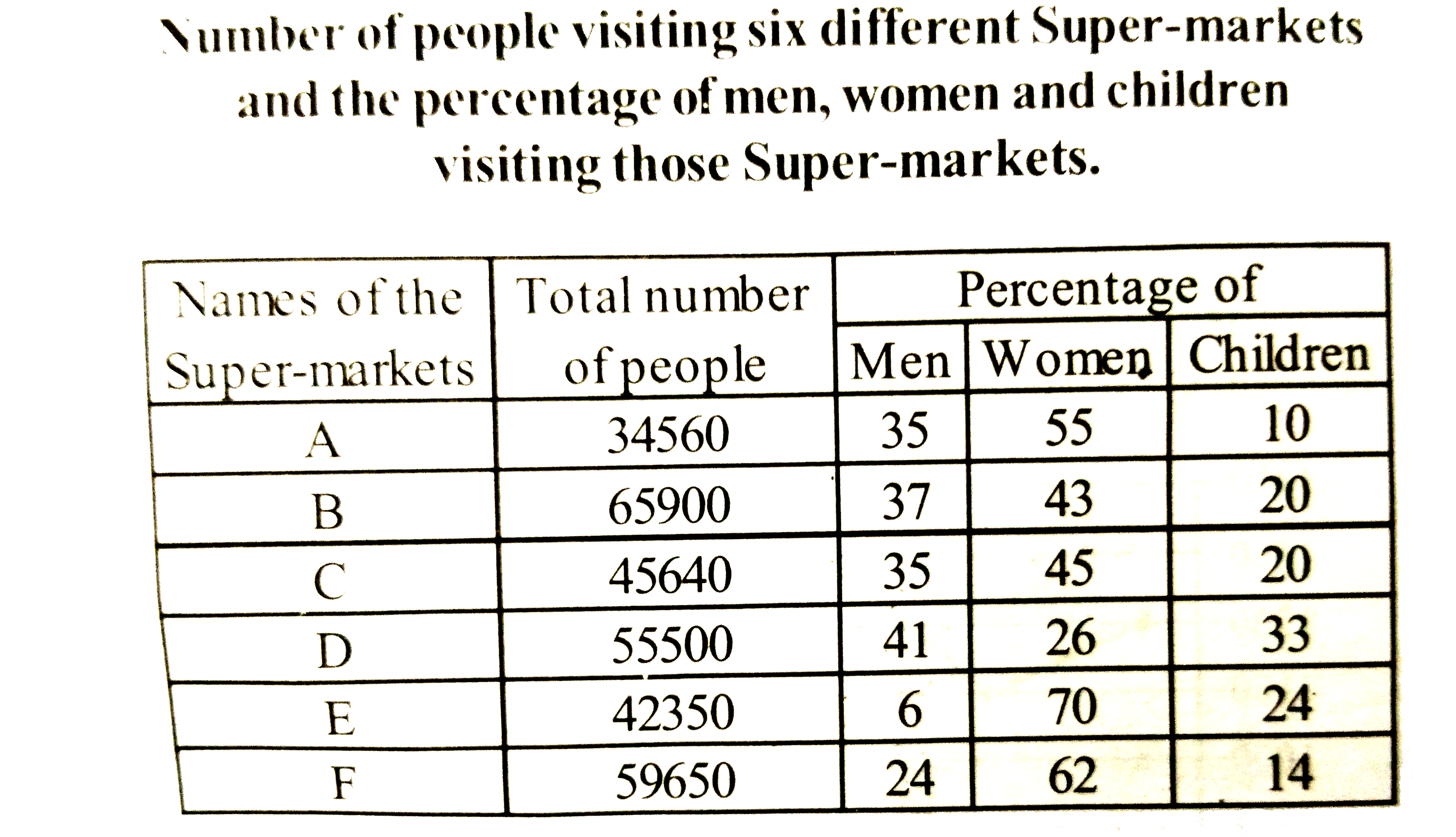
What is the total number of children visiting Super-markets B and D together ?
View Solution
