If A, B are two sets, prove that $A \cup B = (A - B) \cup (B - A) \cup (A \cap B)$ .
Hence or otherwise prove that
$n (A \cup B) = n (A) + n (B) - n (A \cap B)$
where, n(A) denotes the number of elements in A.

Video Solution

Text Solution

Verified by Experts

Let $x \in A \cup B \Rightarrow x \in A or x \in B$
iff(x inAandxcancelinB)or(x inBandxcancelinA)
or $(x \in A and x \in B)$ [from definition of union]
$\Leftrightarrow x \in (A - B) or x \in (B - A) or x \in A \cap B$
$\Leftrightarrow x \in (A - B) \cup (B - A) \cup (A \cap B)$
$∴ A \cup B \subseteq (A - B) \cup (B - A) \cup (A \cap B)$
and $(A - B) \cup (B - A) \cup (A \cap B) \subseteq A \cup B$
Hence, $A \cup B = (A - B) \cup (B - A) \cup (A \cap B)$
Let the common elements in A and B are z and only element of A are x (represented by vertical lines in the Venn diagram) and only element of B are y (represented by horizontal lines in the Venn diagram)

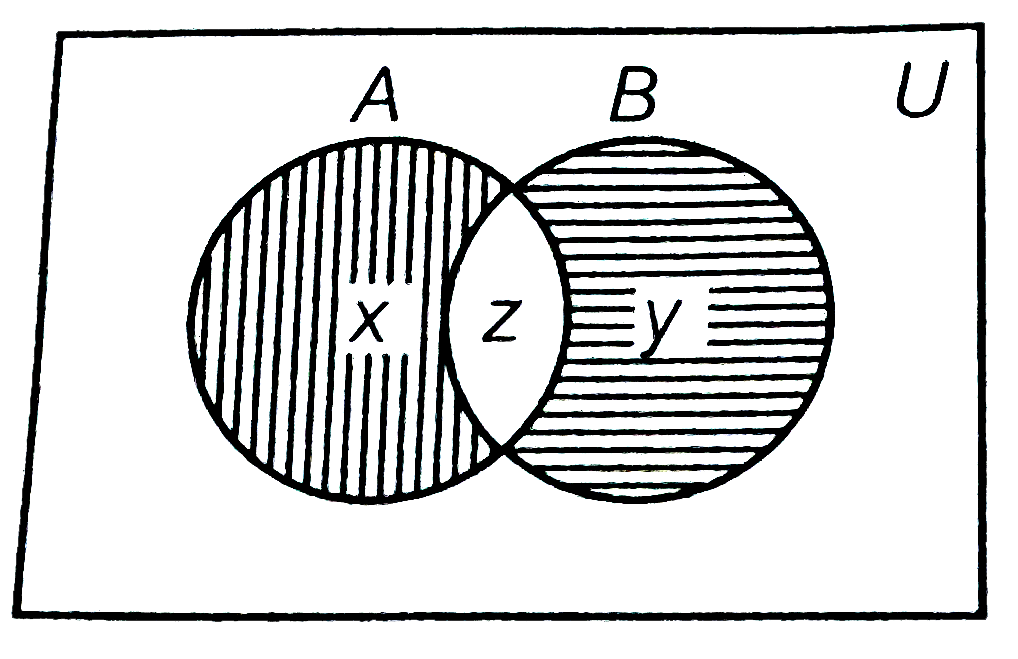
$∴ n (A)$ = Total elements of A = x + z
n(B) = Total elements of B = y + z
$n (A \cap B)$ = Common elements in A and B = z
Now, $n (A \cup B)$ = Total elements in complete region of A and B
x + y + z
$= (x + z) + (y + z) - z$
$= n (A) + n (B) - n (A \cap B)$
Hence, $n (A \cup B) = n (A) + n (B) - n (A \cap B)$

Updated on:21/07/2023

If A and B are two sets, then $(A \cup B)' \cup (A' \cap B)$ is equal to
A $A'$
B $A$
C $B'$
DNone of these
In $n (A) = 3, n (B) = 6 and A \subseteq B$ then the number of elements in $A \cup B$ is equal to
A3
B9
C6
DNone of these
If A and B are two sets, then $(A \cup B)' \cup (A' \cap B)$ is equal to
AA'
BA
CB
DNone of these