If R is a relation from a set A to a set B and S is a relation from B to a set C, then the relation $S o R$

A

is from A to C

B

is from C to A

C

does not exist

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

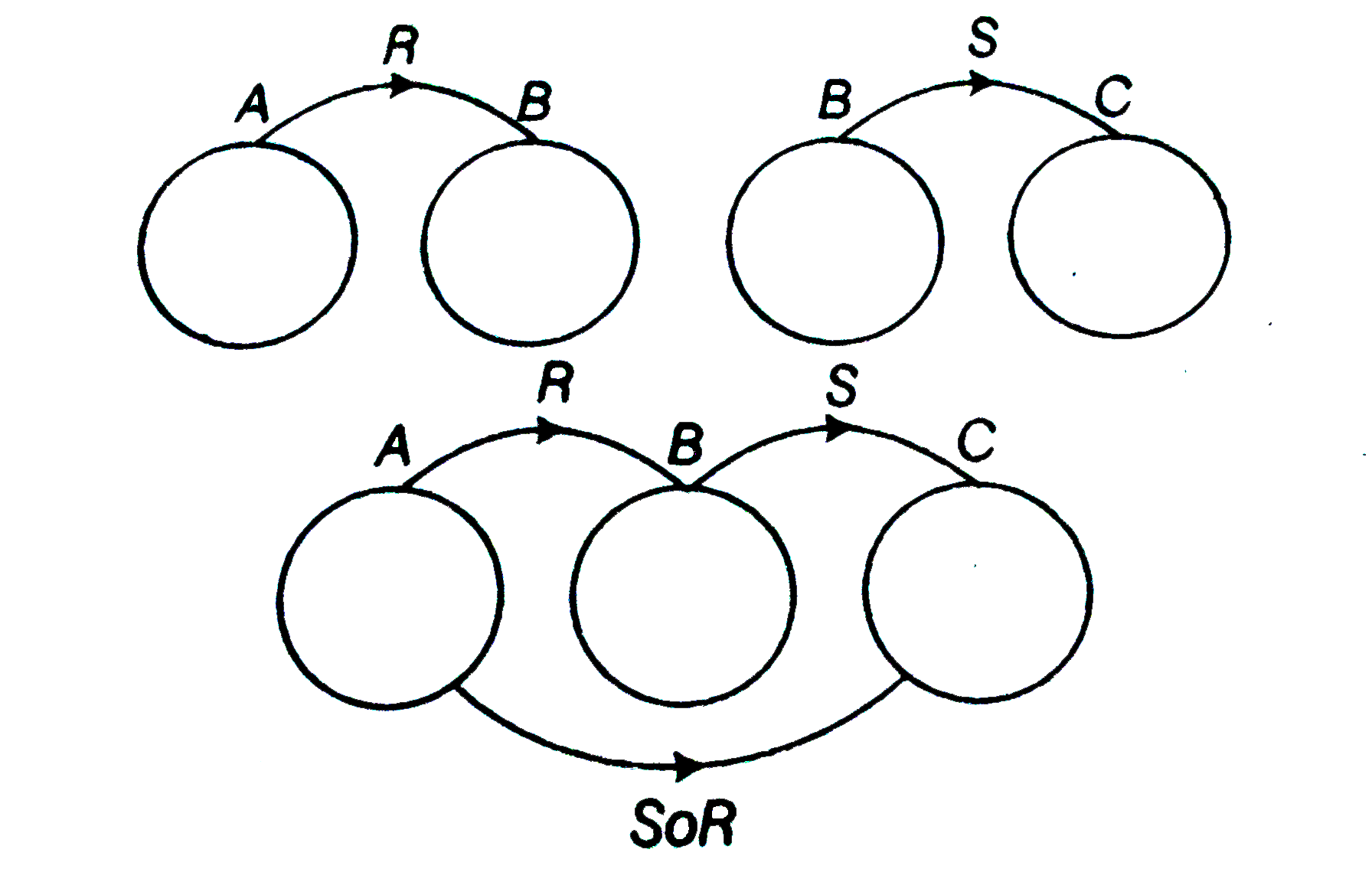
SoR is the relation from A to C.

|

Updated on:21/07/2023

Class 12 MATHS SETS, RELATIONS AND FUNCTIONS

Topper's Solved these Questions

BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (More Than One Correct Option Type Questions)
3videos
SETS, RELATIONS AND FUNCTIONS
BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Passage Based Questions)
6videos
SETS, RELATIONS AND FUNCTIONS
BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 3
10videos
SETS, RELATIONS AND FUNCTIONS
BOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38videos
SEQUENCES AND SERIES
BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18videos
THE STRAIGHT LINES

Similar Questions

Knowledge Check

Question 1 - Select One
If S is a relation on a set A, then
AA= S
B $S = A \times A$
C $S \subseteq A \times A$
D $A \subseteq S \times S$
Question 2 - Select One
Let $R$ be a relation from a set $A \to$ a set B, then $R = A \cup B$ b. $R = A \cap B$ c. $R \subseteq A \times B$ d. $R \subseteq B \times A$
A $R = A \cup B$
B $R = A \cap B$
C $R \subseteq A \times B$
D $R \supseteq B \times A$
Question 3 - Select One
If $R$ is a relation from a finite set A having $m$ elements to a finite set B having $n$ elements then the number of relations from A to B is $2^{m n}$ b. $2^{m n} - 1$ c. . d. $m^{n}$
A $2^{m n}$
B $2^{m n} - 1$
C $2 m n$
D $m^{n}$

ARIHANT MATHS-SETS, RELATIONS AND FUNCTIONS -Exercise (Single Option Correct Type Questions)

Home
Ask Doubt
Profile