Use the arbitrary method to balance the following equations:
a. $K I O_{3} + K I + H_{2} S O_{4} \to K I_{3} + K_{2} S O_{4} + H_{2} O$
b. $P b {(N_{3})}_{2} + C o {(M n O_{4})}_{3} \to C o O + M n O_{2} + P b_{3} O_{4} + N O$
c. $K_{4} [F e {(C N)}_{6}] + K O H + C e {(N O_{3})}_{4} \to F e {(O H)}_{3} + C e {(O H)}_{3} + K_{2} C O_{3} + K N O_{3} + H_{2} O$

Video Solution

Text Solution

Verified by Experts

$a K I O_{3} + b K I + c H_{2} S O_{4} \to d K I_{3} + e K_{2} S O_{4} + f H_{2} O$
$a + b = d + 2 e$ (balancing the $K$ atoms)…(i)
$a + b = 3 d$ (balancing the $I$ atoms)…..(ii)
$c = e = f$ (balancing the $H$ and the $S$ atoms)……(iii)
$3 a + 4 c = 4 e + f$ (balancing the $O$ atoms)….(iv)
Combining equations (iii) and (iv)
$3 a = f$
Let $a = 1$ , then $c = e = f = 3$
Substracting equation (i) from equation (ii)
$d = e = 3$
Hence, $b = 3 (3) - 1 = 8$
The combination equation is
$K I O_{3} + 8 K I + 3 H_{2} S O_{4} - 3 K I_{3} + 3 K_{2} S O_{4} + 3 H_{2} O$
b. $a P b {(N_{3})}_{2} + b C o {(M n O_{4})}_{3} \to c C o O + d M n O_{2} + e P b_{3} O_{4} + f N O$
$∴ a = 3 e$ (balancing $P b$ atoms)....(i)
$6 a = f$ (balancing $N$ atoms).....(ii)
$b = c$ (balancing $C o$ atoms)....(iii)
$3 b = d$ ( balancing $M n$ atoms)....(iv)
$12 b = c + 2 d + 4 e + f$ (balancing $O$ atoms)....(v)
Combining eqautions (i) and (ii)
$6 a = f = 18 e$
Combining eqautions (iii), (iv), and (v)
$12 b = 4 d = 12 c = c + 2 d + 4 e + f$
Let $a = 1$ , then $f = 6, 18 e = 6$ , so $e = \frac{1}{3}$
From equation (v)
$4 d = c + 2 d + 4 e + f$
$4 d = \frac{1}{3} d + 2 d + 4 \times \frac{1}{3} + 6$
$∴ 4 d - \frac{1}{3} d - 2 d = \frac{4}{3} + 6$
$∴ d = \frac{22}{5}$
Similarly from eqaution (v)
$12 b = 4 d = 4 \times \frac{22}{5} = \frac{88}{5 \times 12} = \frac{22}{15}$
Hence, the coefficients are
$a = 1, b \frac{22}{15}, c = \frac{1}{3} d = \frac{1}{3} \times \frac{22}{5} = \frac{22}{15}$
$d = \frac{22}{5}, e = \frac{1}{3}, f = 6$
Multiply each of these values by $30$ to obtain the intergral ratio
$a : b : c : d : e : f = 30 : 44 : 44 : 132 : 10 : 180$ $30 P b {(N_{3})}_{2} + 44 C o {(M n O_{4})}_{3} \to 44 C o O + 132 M n O_{2} + 10 P b_{3} O_{4} + 180 N O$
c.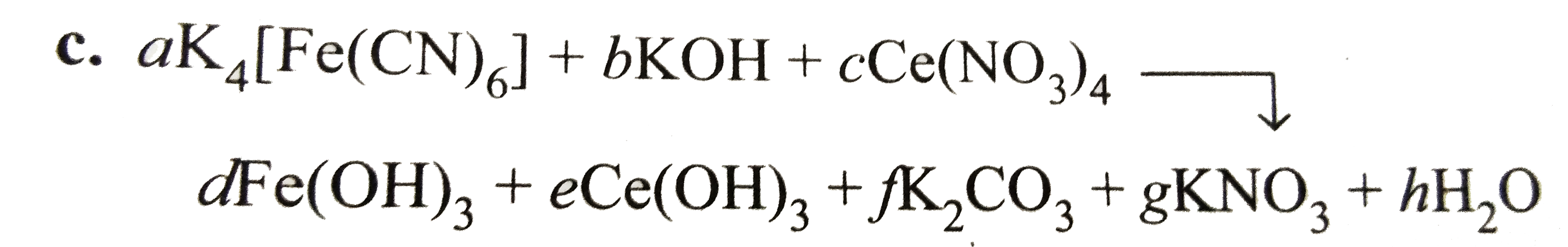
$∴ 4 a + b = 2 f + g$ (balancing $K$ atom).....(i)
$a = d$ (balancing $F e$ atoms)....(ii)
$6 a = f$ (balancing $C$ atoms).....(iii)
$6 a + 4 c = g$ (balancing $C$ atoms).....(iv)
$b + 12 c = 3 d + 3 e + 3 f + 3 g + h$ (balancing $O$ atoms)....(v)
$b = 3 d + 3 e + 2 h$ (balancing $H$ atoms)....(vi)
Solve the eqaution and simplify to obtain the integral ratios.
$a : b : c : d : e : f : g : h = 1 : 258 : 61 : 1 : 6 : 250 : 36$
Hencek the complete equaiton is
.

|

Updated on:21/07/2023

Class 11 CHEMISTRY REDOX REACTIONS

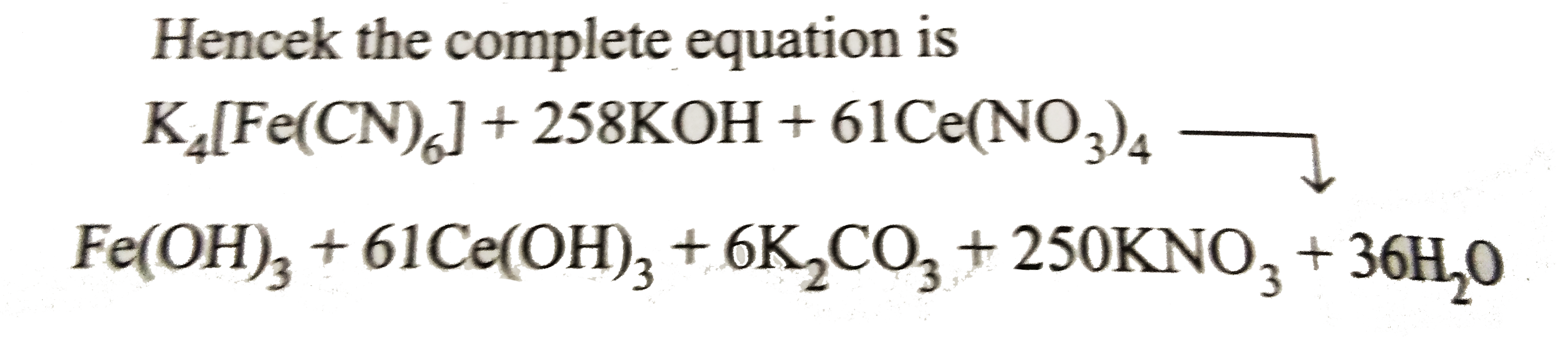Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the following reaction:
$x K M n O_{4} + y N H_{3} \to K N O_{3} + M n O_{2} + K O H + H_{2} O$
$x$ and $y$ are
A $x = 4$ , $y = 6$
B $x = 8$ , $y = 3$
C $x = 8$ , $y = 6$
D $x = 3$ , $y = 8$

CENGAGE CHEMISTRY-REDOX REACTIONS-Archives (Integers)

Home
Ask Doubt
Profile