ψ2 determine the probability of finding the electron in particular region of sapce
1
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRYCHAPTER - ATOMIC STRUCTUREEXERCISE - Archives (Linked Comprehension
3 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRYCHAPTER - ATOMIC STRUCTUREEXERCISE - Archives Multiple Correct
7 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRYCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises Fill In The Balnks
56 Videos
- APPENDIX - INORGANIC VOLUME 1BOOK - CENGAGE CHEMISTRYCHAPTER - APPENDIX - INORGANIC VOLUME 1EXERCISE - chapter-7 Single correct answer
1 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
Similar Questions
Knowledge Check
The probability of finding the electron in the orbital is
A100%B90−95%C70−80%D50−60%The probability of finding the electron in the orbital is
Azero at the nucleusBMaximum on two opposite sides of the nucleus along X-axisCZero on Z-axisDsame on all sides around the nucles.The probability of finding the electron in Px orbital is
Amaximum on two opposite sides of the nucleus along X-axisBzero at the nucleusCthey produces heating effectDthey can affect photographic plate.
The probability of finding an electron in an orbital is approximately?
View SolutionThe zero probability of finding the electron in dx2−y2 orbital is
View SolutionThe zero probability of finding the electron in dx2−y2 orbital is
View SolutionThe zero probability of finding the electron in dx2−y2 orbital is
View SolutionThe Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Psi_(2s) = ((Z)/(2a_(0)))^(½) (1-(Zr)/(a_(0)))e^(-(Zr)/(a_(0)))
The plot of radial probability function 4πr2R2 aganist r will be:
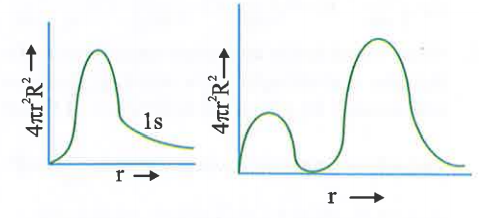
Answer the following questions:
The following graph is plotted for ns-orbitals
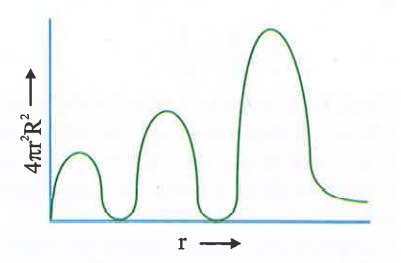
The value of 'n' will be:
View Solution
