Draw a two-dimesnsional haxagonal lattice. Try to visualize the possibility of pentagonal two-dimensional lattice.
Video Solution
Text Solution
Three regular haxagons intersect at one point. So, in this two-dimensional lattice, this lattice point is shared by three unit cells.
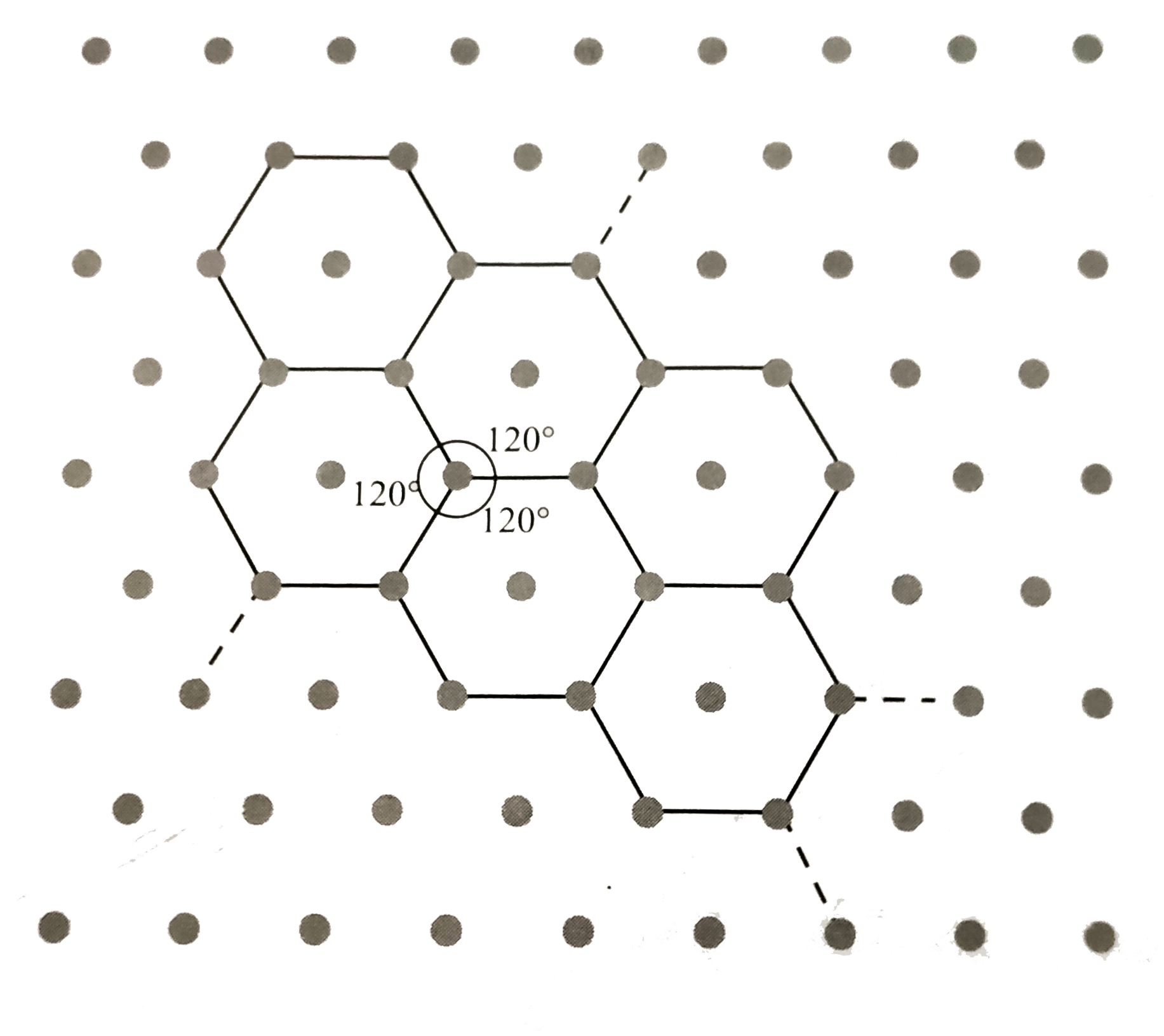
So, the effective number of lattice point per unit cell =6×(13)+1×(1)=3.
A regular pentagon has an interior angle of 108∘, pentagons cannot be made to meet at a point bearing a constant angle to one another. Hence, a pentagonal lattice is not possible. On the other hand, a square or a hexagonal two-dimensional lattice is possible as their internal angles add up to give 360∘.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Solved Examples13videos
SOLID STATE
- BOOK - CENGAGE CHEMISTRYCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)13videos
SOLID STATE
- BOOK - CENGAGE CHEMISTRYCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE3videos
REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDS
- BOOK - CENGAGE CHEMISTRYCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)9videos
SOLUTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of possible three dimensional lattices are :
A7B14C6D8 - Question 2 - Select One
Three-dimensional close packing in solids is referred to as stacking the second square closed packing exactly above the first. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other. This can be done in two ways. Three-dimensional close packing from two-dimensional square close-packed layers: By putting the second square closed packing exactly above the first, it is possible to form three-dimensional close packing. In this tight packing, the spheres are horizontally and vertically correctly balanced. Similarly, we can obtain a simple cubic lattice by adding more layers, one above the other.Three-dimensional close packing from two-dimensional hexagonal close-packed layers: With the assistance, of two-dimensional hexagonal packed layers, three-dimensional close packing can be obtained.
What will be the ratio of radii of the spheres in cubic systems simple cubic, body centred cubic and face centred cubic systems. if 'a' stands for the edge length.A12a:√34a:12√2aB12a:√3a:1√2aC1a:√3a:√2aD12a:√32a:√22a - Question 3 - Select One
How many three dimensional lattices are possible ?
A12B13C14D15
Name any two non dimensional constant.
View SolutionGive two examples of two dimensional motion.
View SolutionHow many types of two-dimensional lattice exist? Why pentagonal latticis not possible?
View SolutionState True or False:
The solid shapes are of two dimensional.View SolutionHow many three dimensional lattices are possible?
View Solution

