If 80% of a radioactive element undergoing decay is left over after a certain periof of time t form the start, how many such periofs should elapse form the start for just over 50% of the element to be left over?
The correct Answer is:3
Let a=100,(a−x)=80 (Amount left).
∴ Amount left =a(2)n,[n=number of half lives]
80=100(2)n⇒(2)n=108
∴nlog2=log10−3log2=1−3×0.3=0.1
n=0.1log2=0.10.3=13
n=13=t(Time for 80% amountleft or 20% decomposed)t1/2(Time for 50% amountleft or decomposed)⇒t1/2=3t
Alternatively
t30%(left)t1/2(left)=log(10080)0.3=13
t1/2=3t80%(left)=3t
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Fill In The Blanks
37 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises True/False
29 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRYCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Assertion-Reasoning
22 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRYCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Radioactive elements is spread over a room, its half life is 30 day, Its activity is 50 times the permissible value. After how many days will it be safe?
View SolutionA radioactive sample undergoes decay as per the following gragp. At timet=0, the number of undecayed nuclei is N0. Calculate the number of nuclei left after 1h.
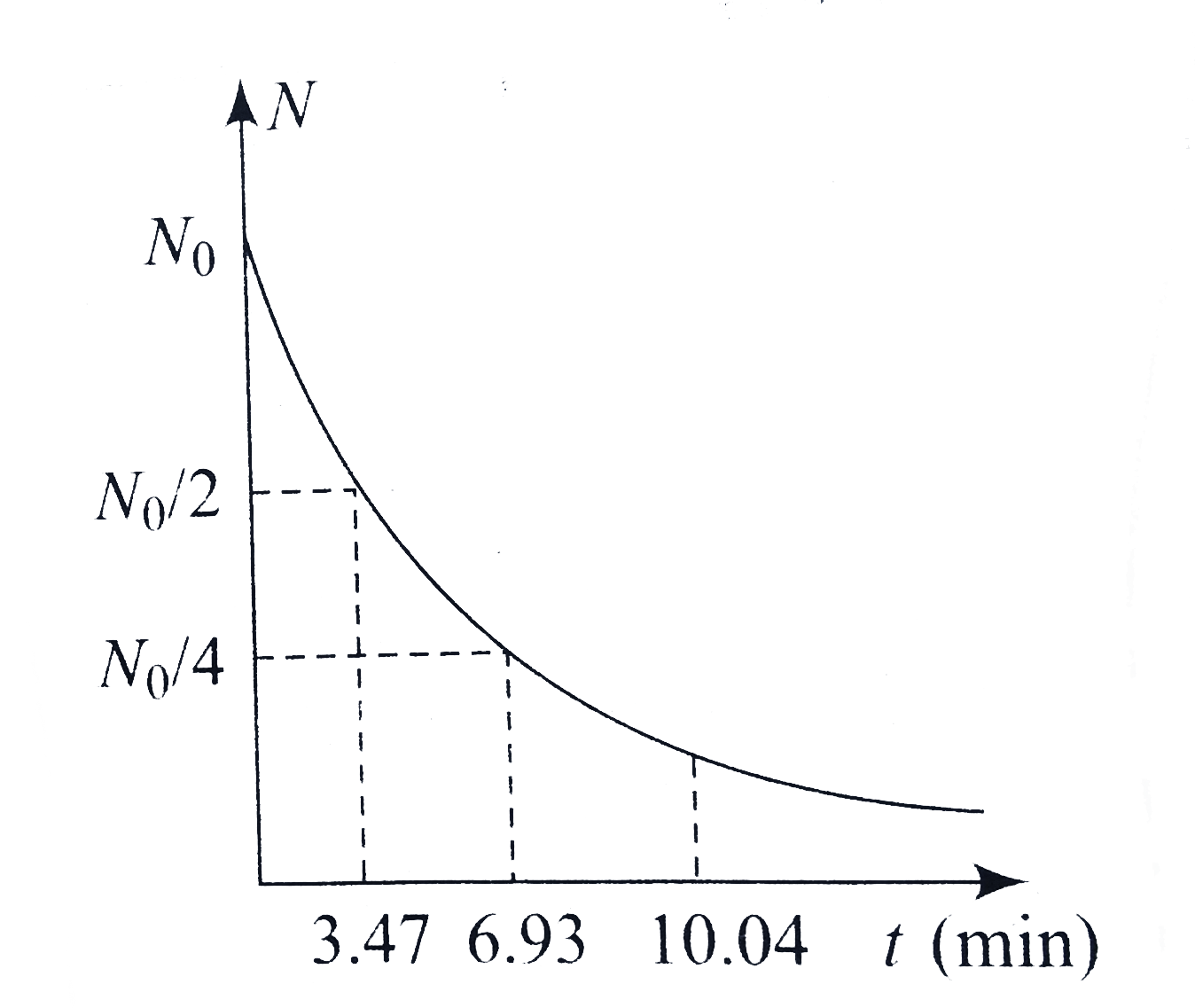 .
.
View Solution
Knowledge Check
A radioactive element undergoing decay is left 20% of its initial weight after certain period of time t. How many such periods should elapse from the start for the 50% of the element to be left over?
A3B4C5Dnone of theseThe half life of the radioactive element is 35 years. If there are 4×106 nuclei at the start then after how many years 0.5×106 of them would be left ?
A35B70C105D140The initial mass of a radioactive element is 40g. How many grams of it would be left after 24 years if its half− life period I s of 8 years ? a)2 b)5 c)10 d)20
A2B5C10D20
A radioactive element gets spilled over the floor of a room. Its half life period is 30 days. If the initial activity is ten times the permissibel value, after how many days will it be safe to enter the room?
View SolutionA radioactive element gets spilled over the floor of a room. Its half life period is 30 days. If its initial activity is ten times the permissible value, after how many days will it be safe to enter the room?
View SolutionA radioactive element gets spilled over the floor of a room. Its half-life period is 30 days. If the initial activity is ten times the permissible value, after how many days will it be safe to enter the room ?
View SolutionThe initial mass of a radioactive element is 40g. How many grams of it would be left after 24 years if its half− life period I s of 8 years ?
View Solution90% of a radioactive sample is left undecayed after time t has elapsed. What percentage of the initial sample will decay in a total time 2t ?
View Solution