Assertion (A): In radioactive disintegrations, .2H4 nuclei can come out of the nucleus but lighter .2H3 cannot.
Reason (R): The binding energy of .2H3 is more than that of .2H4.
If both (A) and (R) are correct , and (R) is the correct explanation of (A)
If both (A) and (R) are correct, but (R) is not the correct explanation of (A)
If (A) is correct, but (R) is incorrect.
If (A) is incorrect, but (R) is correct.
The correct Answer is:C
Radioactive disintegration reaction produces stable nuclei, till that the nuclei undergo the process. The .2He4 nuclei is more stable than .2He3 nuclei. Hence, it is proceed in radioactive reaction.
Topper's Solved these Questions
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRYCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Exercise Fill In The Blanks
30 Videos
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRYCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Exercise True/False
20 Videos
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRYCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Exercises Single Correct
80 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRYCHAPTER - NCERT BASED EXERCISEEXERCISE - Nuclear Chemistry (NCERT Exercise)
29 Videos
- ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPBOOK - CENGAGE CHEMISTRYCHAPTER - ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPEXERCISE - Archives Analytical And Descriptive
24 Videos
Similar Questions
Knowledge Check
Assertion (A): In radioactive disintegrations, .2He4 nuclei can come out of the nucleus but lighter .2H3 cannot.
Reason (R): The binding energy of .2H3 is more than that of .2H4.ASTATEMENT-1 is True, STATEMENT-2 is True, STATEMENT-2 is correct explanation for STATEMENT-1BSTATEMENT-1 is True, STATEMENT-2 is True, STATEMENT-2 is NOT a correct explanation for STATEMENT-1CSTATEMENT-1 is True, STATEMENT-2 is FalseDSTATEMENT-1 is False, STATEMENT-2 is TrueAssertion : Bond angle in H2O is less than that in H2S.
Reason : Electronegativity of O is more than that of S.AAssertion and reason both are correct statements and reason is correct explanation for assertion.BAssertion and reason both are correct statements but reason is not correct explanation for assertion.CAssertion is correct statement but reason is wrong statement.DAssertion is wrong statement but reason is correct statement.Assertion (A):
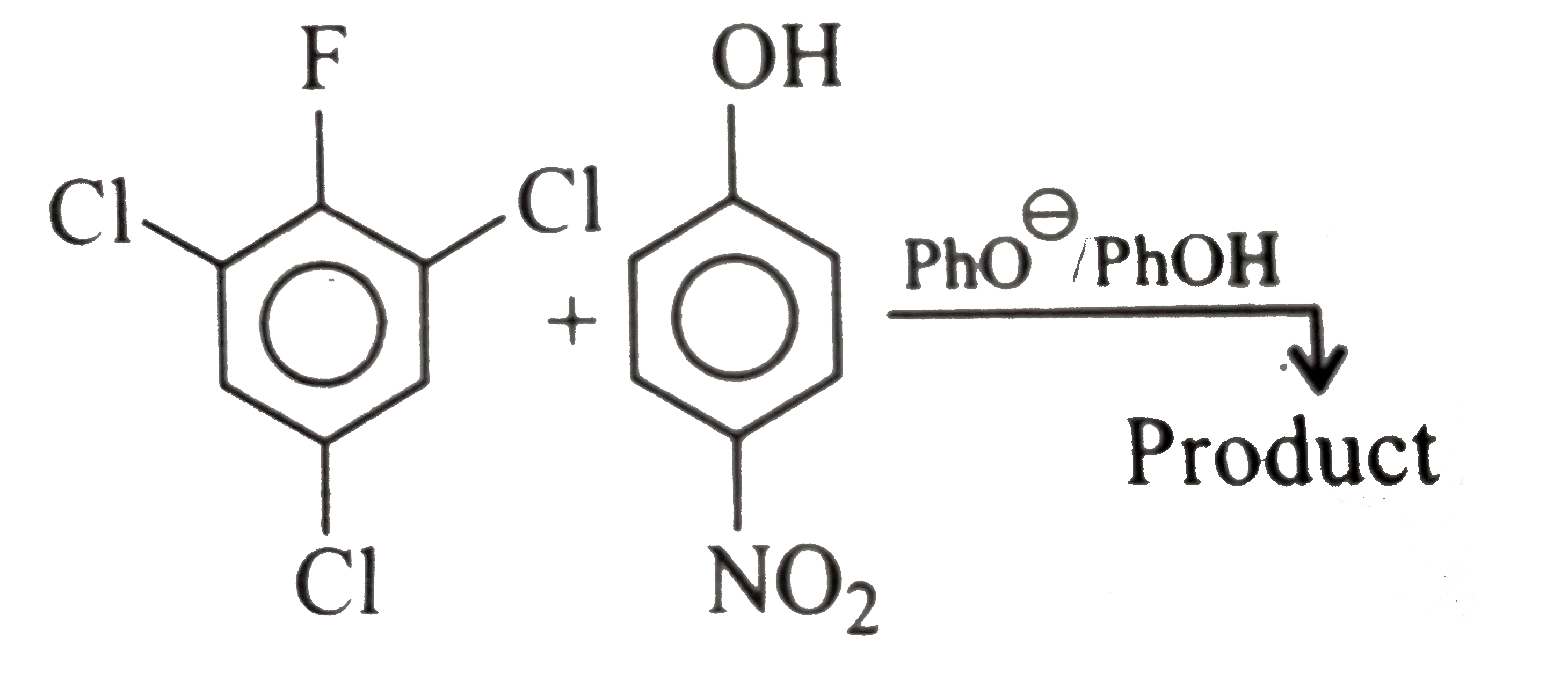
The product is: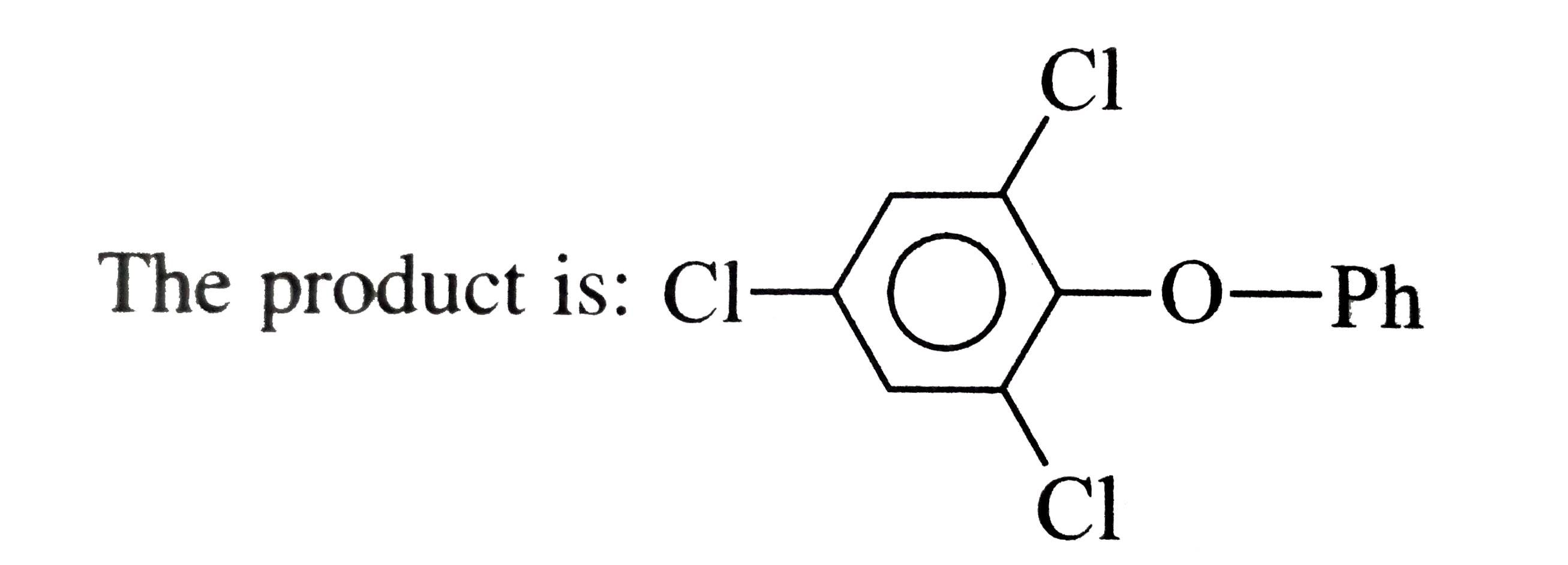
Reason (R ): p−NO2−C6H4O− is a stronger nucleophile than PhO−.AIf both (A) and (R ) are true and (R ) is the correct explanation of (A).BIf both (A) and (R ) are true but (R ) is not the correct explanation of (A).CIf (A) is true but (R ) is false.DIf both (A) and (R ) are false.
Given reason for the following :
H+2andH−2 ions have the same bond order but H+2 ions are more stable thanH−2 .
View SolutionWhy H2 is more stable than H+2 while He+2 is more stable than He2 ?
View SolutionAssertion: Out of 1He3 and 7He3, the binding energy of 1He3 is greater than 2He8.
Reason: Inside the nucleus of1H3, there is more repulsion than inside the nucleus of 2He4.
View SolutionAssertion: Ca++ cannot replace H+ adsorbed on clay or humus particles.
Reasoning: The retentive capacity of Ca+2 is more than that of H+.
View SolutionAssertion (A) : H2S is more acidic than H2O.
Reason (R) :H-S bond is more polar than H-O bond.
View Solution
