माना A={−1,1,2} तथा B={1,16} तथा f:A→B पर एक फलां इस प्रकार परिभाषित है, की f(x)=x4 दिखाइए की यह फलां आच्छादक ( onto ) है ।
दिया है : f:A→B v f(x)=x4
इसलिए f(−1)=(−1)4=1
f(1)=(1)4=1
f(2)=(2)4=16
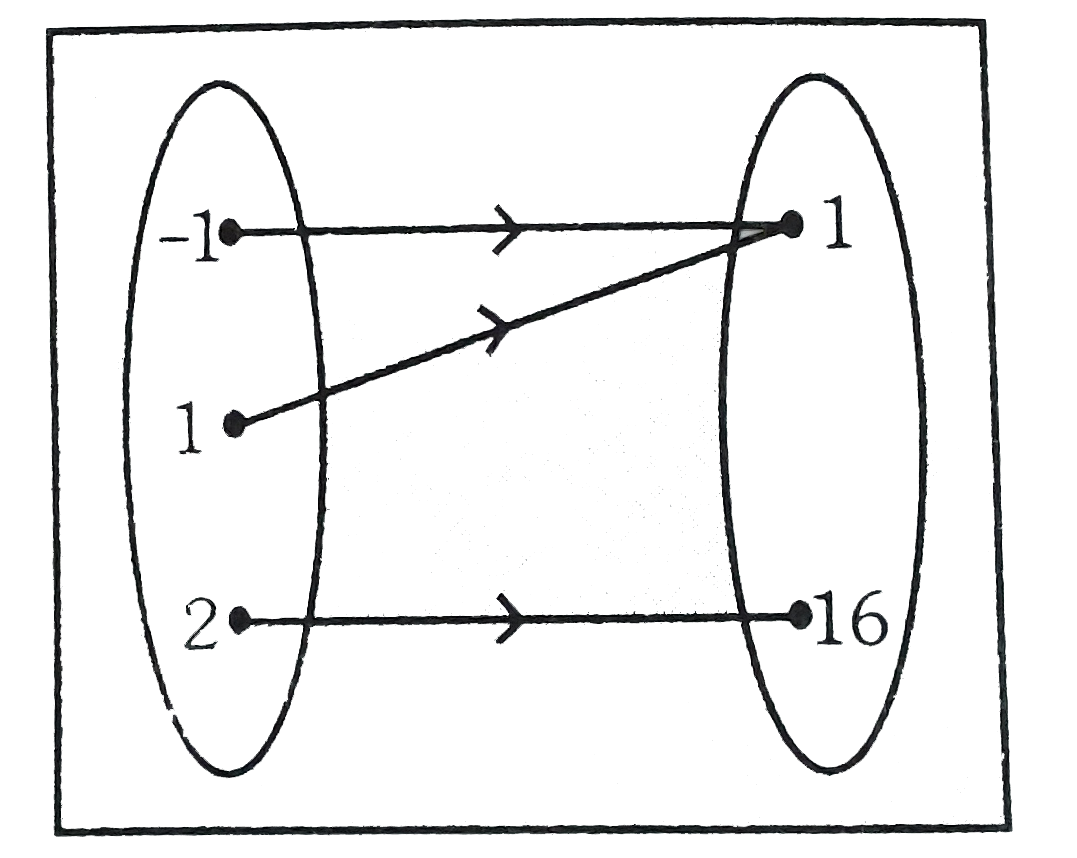
स्पष्ट है, की
(i) के पूर्व प्रतिचित्रण 1 व् -1 है
(ii) 16 का पूर्व प्राचित्रण 2 है व् B के अंदर एक भी ऐसा अवयव नहीं है जो A में पूर्वक प्रतिबम्ब न रखता है ।
इसलिए f एक आच्छादक फलां है
Topper's Solved these Questions
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.1
2 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.2
6 Videos
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - स्वमूल्यांकन परीक्षण
10 Videos
- सदिश बीजगणित BOOK - BALAJI PUBLICATIONCHAPTER - सदिश बीजगणित EXERCISE - स्वमूल्यांकन परीक्षण
23 Videos
Similar Questions
वास्तविक संख्याओं के समुछ्य S में सम्बन्ध R इस प्रकार परिभाषित है की R={(a,b):(1+ab)>0} सिद्ध कीजिय की R, सावतुल्य व् सम्मिट है परन्तु क्रनक्रम नहीं ।
View Solutionयदि R वास्तविक संख्याओं का समुछ्ती है, तो सिद्ध कीजिय कि फलां जो इस प्रकार परिभाषित हो
f:R→R,f(x)=ex,x∈R
एकेकी प्रतिचितरण है
View Solutionनिम्न अवरोधों के अन्तर्गत z = -3x + 4y का न्यूनतमीकरण कीजिए -
x+2y≤8,3x+2y≤12,x≥0,y≥0
View Solutionसदिश →a=ˆi−2ˆj+ˆk,→b=−2ˆi+4ˆj+5ˆk और →c=ˆi−6ˆj−7ˆk का योगफल ज्ञात कीजिए।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएक पुस्तकालय को एक शेल्फ में दो भिन्न प्रकार की पुस्तकें रखनी है| पुस्तकें क्रमशः 6 सेमि और 4 सेमि मोती है| तथा उसका भार क्रमशः 1 किग्रा और 112 किग्रा है| शेल्फ 96 सेमि लम्बी है तथा अधिकतम 21 किग्रा भार सेह सकती है|शेल्फ दो प्रकार की पुस्तकों से किस प्रकार भरा जाएँ ताकि उसमें अधिकतम पुस्तकें रखी जा सकें?
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionसिद्ध कीजिये x>0 की के लिए f(x)=1x हस्यमान फलां है।
View Solutionसिद्ध कीजिये की फलन f(x)=tan−1x−x,x∈R के लिए फलां हस्यमान है।
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionमाना A तथा B दो घटनाऐं इस प्रकार है कि P(A∩B)=16,P(A∪B)=3145 तथा P(¯¯¯B)=710 तब
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solution
