एक कम्पनी A और B नमूने की दो चमड़े की बेल्ट बनाती हैं । बेल्ट A उच्च कोटि की एंव बेल्ट B घटिया कोटि की हैं । दोनों बेल्टों पर लाभ क्रमशः 40 तथा 30 रुपये प्रति बेल्ट हैं । A प्रकार की एक बेल्ट के बनाने में B किस्म की एक बेल्ट बनाने से दोगुना समय लगता हैं । यदि सब बेल्ट B नमूने की हों तो कम्पनी 1000 बेल्ट प्रतिदिन बना सकती हैं । लेकिन चमड़े की पूर्ति केवल 800 ( A और B दोनों को मिलाकर ) बेल्ट प्रतिदिन के लिए पर्याप्त हैं । बेल्ट A के लिए एक फेन्सी बक्कल चाहिए और उसके लिए केवल 400 बक्कल प्रतिदिन प्राप्त हैं । बेल्ट B के लिए केवल 700 बक्कल प्रतिदिन प्राप्त है । अधिकतम लाभ के लिए कम्पनी दोनों तरह की बेल्ट कितनी बनाए , आलेख विधि से हल करते हुए ज्ञात कीजिए ?
समस्या के आँकड़ो के अनुसार यदि हम मान लें कि कंपनी A प्रकार की x1 तथा B प्रकार की x2 बेल्ट बनाती हैं । अब दिया गया है कि A तथा B नमूने की प्रत्येक बेल्ट पर लाभ क्रमशः 40 रुपये तथा 30 रुपये हैं । अतः कम्पनी के कुल लाभ z के लिए
z=40x1+30x2
चूँकि किस्म के एक बेल्ट के बनाने में किस्म के एक बेल्ट से दोगुना समय लगता हैं तथा यदि सभी किस्म की बेल्ट बनाऊ जायें तो कम्पनी प्रतिदिन केवल 1000 बेल्ट तैयार कर सकती हैं । अतः
2x1+x2≤1000
साथ ही A तथा B किस्म की बेल्ट बनाने के लिए केवल 800 बेल्ट प्रतिदिन बनाने का चमड़ा उपलब्ध हैं अतः x1+x2≤800
पुनः A किस्म की बेल्ट बनाने के लिए केवल 400 बक्कल प्रतिदिन उपलब्ध हैं अतः x1≤400 इसी प्रकार x2≤700 अन्त में बेल्टों के उत्पादन की संख्या ऋणात्मक नहीं हो सकती
x1≥0 तथा x2≥0
उपर्युक्त समस्या का गणितीय निरुपण निम्न हैं -
अधिकतम करो z=40x1+30x2
प्रतिबंध 2x1+x2≤1000
x1+x2≤800
x1≤400
x2≤700
x1,x2≥≥0
आलेखी हल : प्रतिबंध की असमिकाओं के संगत सरस रेखाएँ निम्न हैं -
2x1+x2=1000
या (x1500+x21000)=1
x1+x2=1
या (x1800+x2800)=1
उपर्युक्त सरल रेखाओं का एक व्दिविम चित्र में आरेखन करते हैं तथा प्रत्येक असमिका का हल क्षेत्र निर्धारित करते हैं । इसके पश्चात् सभी प्रतिबंध की असमिकाओं के क्षेत्रों का उभयनिष्ठ क्षेत्र OABCDE (छायांकित ) समस्या का सुसंगत हल क्षेत्र प्राप्त होता हैं ।
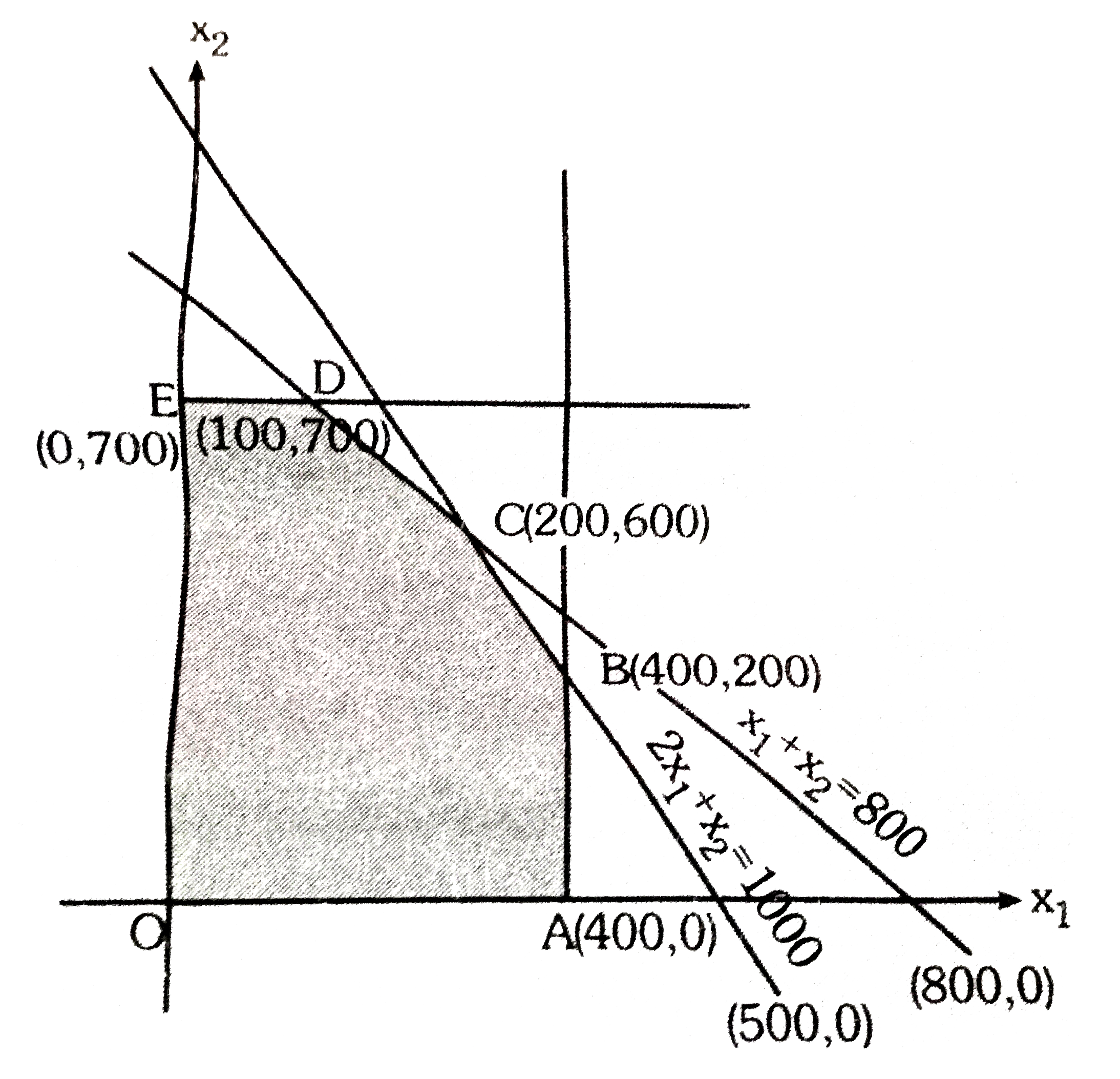
उद्देश्य फलन z में शीर्षों के निर्देशांक प्रतिस्थापित कर इष्टतम हल की परिकल्पना निम्न हैं -
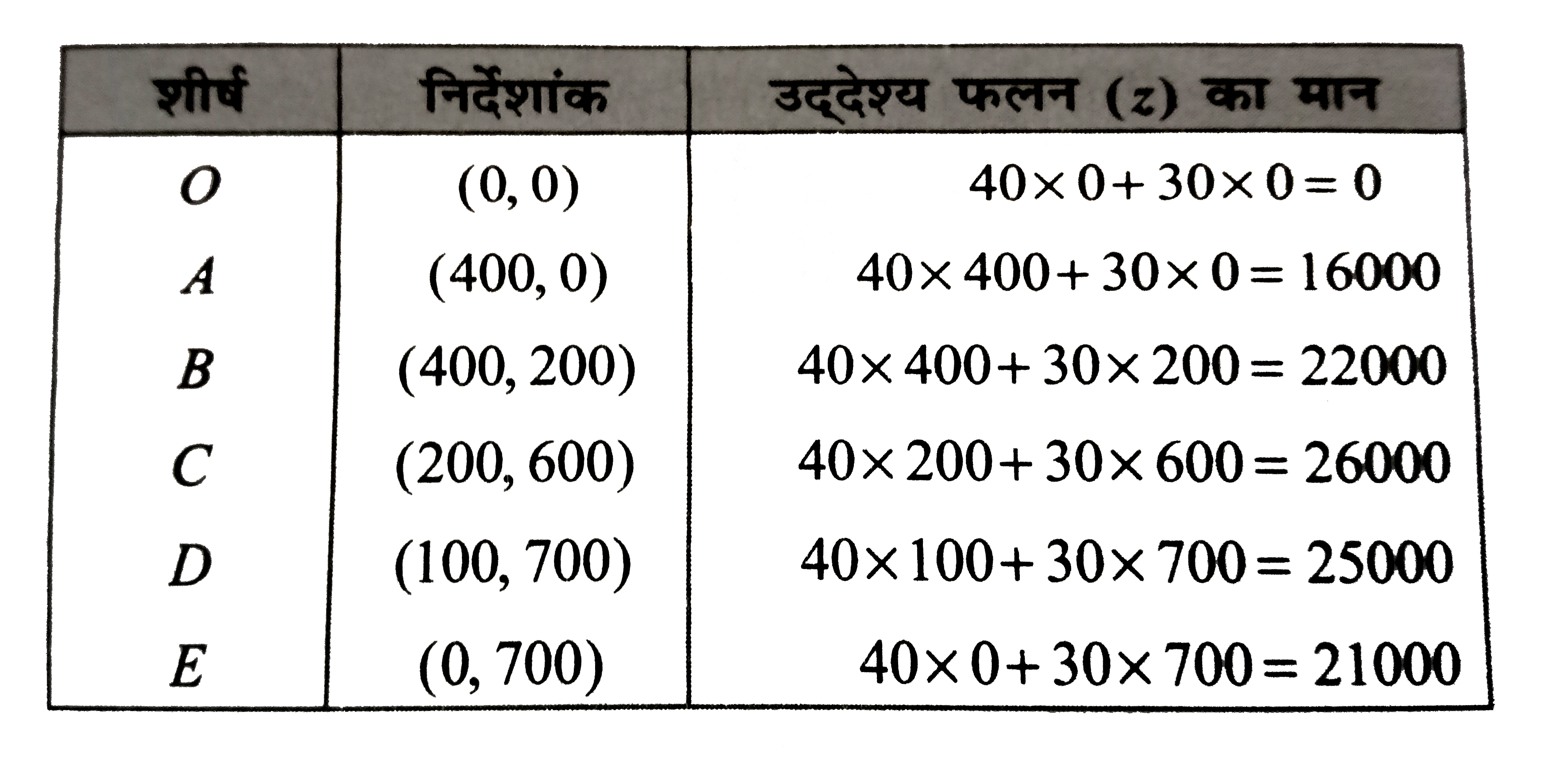
उपर्युक्त तालिका से स्पष्ट हैं कि उद्देश्य फलन z का इष्टतम मान C पर प्राप्त होता हैं ।
अतः समस्या का इष्टतम हल निम्न हैं -
x1=200m,x2=600
तथा अधिकतम लाभ 26000 रुपये ।
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - बहुविकल्पीय प्रश्न
13 Videos
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास प्रश्न 23.1
8 Videos
- प्रायिकता क्रमश:BOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकता क्रमश:EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.3
7 Videos
Similar Questions
रैखिक प्रोग्रामन समस्या निम्न व्यवरोधों के अन्तर्गत x1+2x2≤2000,x1+x2≤1500,x2≤600 और x1,x2≥0 हैं तो कौन - सा बिंदु घिरा हुए धन भाग में नही हैं ?
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
3x1+2x2≤12
5x1≤1
x1+x2≥8
−x1+x2≥4
तथा x1,x2≥0
अधिकतम z=x1+12x2
View Solutionएक प्रश्न-पुस्तिका में 300 सरल सत्य/असत्य प्रश्न, 200 कठिन सत्य/असत्य प्रश्न, 500 सरल बहुविकल्पीय प्रश्न तथा 400 कठिन बहुविकल्पीय प्रश्न है | यदि प्रश्न-पुस्तिका से एक प्रश्न का चयन यदृच्छया किया जाता है | सिद्ध कीजिए कि इस प्रश्न के सरल होने की प्रायिकता 59 है जबकि यह एक बहुविकल्पीय प्रश्न है |
View Solutionवास्तविक संख्याओं के समुछ्य R में प्राचित्रण f(x)=sinx,x∈R तथा g(x)=x2,x∈R द्वारा परिभाषित है सिद्ध कीजिय की gof≠fog
View Solutionएक ही कोटि की दो वर्ग आव्यूहों A तथा B पर विचार कीजिये। निम्न में से कौन-सा कथन सत्य है-
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View Solutionखनिजो के प्रकार |धात्विक खनिज, लोह अयस्क |लोह अयस्क |भारत मे लोह अयस्क के मुख्य बेल्ट |OMR
View Solutionनए की जन्म कुण्डली : एक पाठ के रचनाकार कौन हैं ?
View Solutionमेरे घर में पाँच जोड़ी आँखें हैं माँ की आँखें पड़ाव से पहले ही तीर्थ यात्रा की बस के दो पंचर पहिए हैं। पिता की आँखें लोहसाँय की ठंडी शलाखें हैं बेटी की आँखें मंदिर में दीवट पर ' जलते घी के दो दिए हैं। प्रस्तुत पंक्तियों के कवि.कौन है?
View Solutionमेरे घर में पाँच जोड़ी आँखें हैं माँ की आँखें पड़ाव से पहले ही तीर्थ यात्रा की बस के दो पंचर पहिए हैं। पिता की आँखें लोहसाँय की ठंडी शलाखें हैं बेटी की आँखें मंदिर में दीवट पर ' जलते घी के दो दिए हैं। कविता के अनुसार मेरे घर में कितनी जोड़ी आँखें हैं ?
View Solutionमेरे घर में पाँच जोड़ी आँखें हैं माँ की आँखें पड़ाव से पहले ही तीर्थ यात्रा की बस के दो पंचर पहिए हैं। पिता की आँखें लोहसाँय की ठंडी शलाखें हैं बेटी की आँखें मंदिर में दीवट पर ' जलते घी के दो दिए हैं। कविता के अनुसार किसकी आँखें लोहसाँय की ठण्डी शलाखें हैं?
View SolutionA and B at a distance of 1.7 km apart and they start running towards each other at a speed of 8m/s and 9 m/s respectively. After how much time, will they meet each other?
A और B 1.7 किमी की दूरी पर अलग हैं और वे क्रमशः 8 मीटर /सेकंड और 9 मीटर / सेकंड की गति से एक दूसरे की ओर दौड़ना शुरू करते हैं। कितने समय के बाद, वे एक दूसरे से मिलेंगे?
View SolutionC_xH_y कार्बन और हाइड्रोजन की दहन की ऊष्माएँ क्रमश: a, b और c cal हैं। C_xH_y की संभवन ऊष्मा होगी:
View Solutionकैप्रोलैक्टम में, यदि 'a', इलेक्ट्रॉनों (e^-) के एकाकी युग्मों की संख्या हैं तथा 'b', sp^3 संकरित परमाणुओं की संख्या हैं। a + b का मान क्या है?
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solution
