Question

एक फैक्ट्री दो विभिन्न उत्पादों को बनाने के लिए तीन विभिन्न साधन काम में लेती हैं । साधन A की 20 इकाई , साधन B की 12 इकाई व साधन C की 16 इकाई उपलब्ध हैं । पहले उत्पाद की एक इकाई के लिए साधनों की क्रमशः 2,2,4 इकाईयाँ की आवश्यकता पड़ती हैं । तथा दूसरे उत्पाद के लिए 4,2 और 0 इकाईयों की । यह ज्ञात है कि पहला उत्पाद 3 मुद्रा इकाई प्रति इकाई का तथा दूसरा उत्पाद 3 मुद्रा इकाई प्रति इकाई का लाभ देता हैं । रैखिक प्रोग्रामन समस्या का संरुपण कीजिए तथा लेखाचित्र विधि से बताइये कि अधिकतम लाभ के लिए प्रत्येक उत्पाद की कितनी इकाईयाँ बनायी जायें ?

Explanation

गणितीय संरुपण - माना कि फैक्ट्री प्रथम उत्पाद की x इकाई तथा व्दितीय उत्पाद की y इकाई जाती हैं ।
`therefore` फैक्ट्री का कुल उत्पाद
`rArr` z = 2x + 3y ..(1)
प्रथम उत्पाद की x इकाई तथा व्दितीय उत्पाद की y इकाई के लिए साधन A की 2x + 4y इकाई का उपयोग होगा , अंतः प्रश्नानुसार
`2x + 4y le 20` या `x + 2y le 10` ...(2)
इसी प्रकार दोनों उत्पादों में साधन B की 2x + 2y इकाई का उपयोग होगा । अतः प्रश्नानुसार
` 2x + 2y le 12` या `x + y le 6` ...(3)
इसी प्रकार साधन C के लिए प्रश्नानुसार
`4x + 0y le 16` या `x le 4` ...(4)
अन्त में उत्पादों की इकाई ऋणात्मक नहीं हो सकती
इसलिए `x ge 0 , y ge 0`
अतः समस्या का निम्न गणितीय स्वरुप होगा -
अधिकतम करो z = 2x + 3y
प्रतिबंध `x + 2y le 10`
`x + y le 6`
`x le 4`
तथा `x ge 0, y ge 0 `
आलेखी हल - प्रतिबंध असमिकाओं के संगत निम्न सरल रेखाओं का एक व्दिविम चित्र में आरेखन करते हैं - `x + 2y =10` या `(x)/(10) + (y)/(5) = 1`
x + y = 6 या `(x)/(6) + (y)/(6) =1`
x = 4 , x = 0 या y = 0

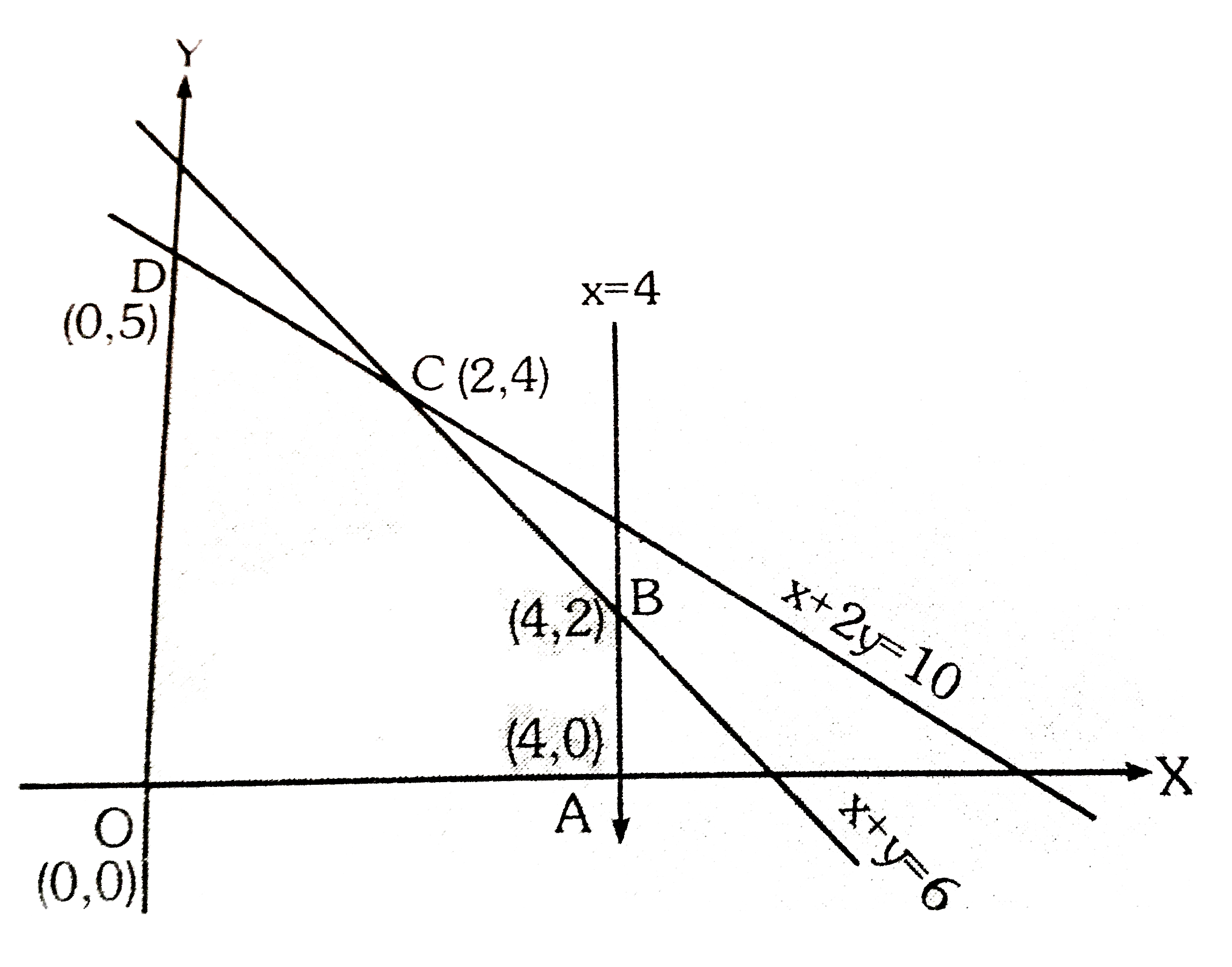
अब लेखाचित्र में प्रत्येक असमिका का हल क्षेत्र निर्धारित कर उनका उभयनिष्ठ हल क्षेत्र देखते हैं । छायांकित बहुभुज क्षेत्र हैं । लेखाचित्र से बहुभुज के शीर्षों के निर्देशांक O(0,0) , A(4,0) , B(4,2) , C(2,4) , D(0,5) हैं ।
उपरोक्त शीर्षों पर उद्देश्य फलन के मान का परिकलन निम्न प्रकार हैं -

उपरोक्त तालिका से स्पष्ट हैं कि उद्देश्य फलन z का अधिकतम मान शीर्ष C (2 ,4 ) पर हैं । अतः प्रथम उत्पाद की 2 इकाई तथा व्दितीय उत्पाद की 4 इकाई बनाने पर 16 मुद्रा इकाई का अधिकतम लाभ होगा ।