एक स्वचालित वाहन निर्माता अपनी फैक्ट्री में जो , दो कार्यशालाओं में विभाजित हैं , मोटर कारें एंव ट्रक बनाता हैं । पहली कार्यशाला में , जहाँ प्रारम्भिक ढाँचे तैयार किये जाते हैं , एक ट्रक के लिए 5 मानव दिवस तथा एक मोटर कार के लिए 2 मानव दिवस लगते हैं । दूसरी कार्यशाला में जिसमें वाहनों को अंतिम रुप दिया जाता हैं , प्रत्येक निर्मित ट्रक या मोटर कार के लिए 3 मानव दिवस लगते हैं । मशीन एंव मानव की सीमाओं के कारण पहली कार्यशाला में 180 मानव दिवस प्रति सप्ताह तथा दूसरी कार्यशाला में 135 मानव दिवस प्रति सप्ताह उपलब्ध हैं । यदि निर्माता को प्रत्येक ट्रक पर 3000 रुपये तथा प्रत्येक मोटर कार पर 2000 रुपये का लाभ हो तो लेखाचित्र विधि से ज्ञात कीजिए कि निर्मााता को अधिकतम लाभ हेतु प्रत्येक प्रकार के कितने वाहन बनाने चाहिए ?
माना वाहन निर्माता x मोटर कार तथा y ट्रक बनाता हैं । तब समस्या का गणितीय निरुपण निम्न प्रकार हैं -
अधिकतम z = 2000x + 3000y
प्रतिबंध
प्रतिबन्ध की असमिकाओं के संगत समीकरण निम्न प्रकार हैं -
2x + 5y = 180
x + y = 45
x = 0 , y = 0
ग्राफ पेपर पर इन रेखाओं को खींचकर उभयनिष्ठ क्षेत्र प्राप्त करते हैं जो चित्र में छायांकित बहुभुज OABC हैं जिसके शीर्ष O(0,0) , A(45, 0) , B(15, 30), तथा C(0, 36 ) पर उद्देश्य फलन के मान क्रमशः 0,90,000 , 1,20,000 तथा 1,08,000 हैं ।
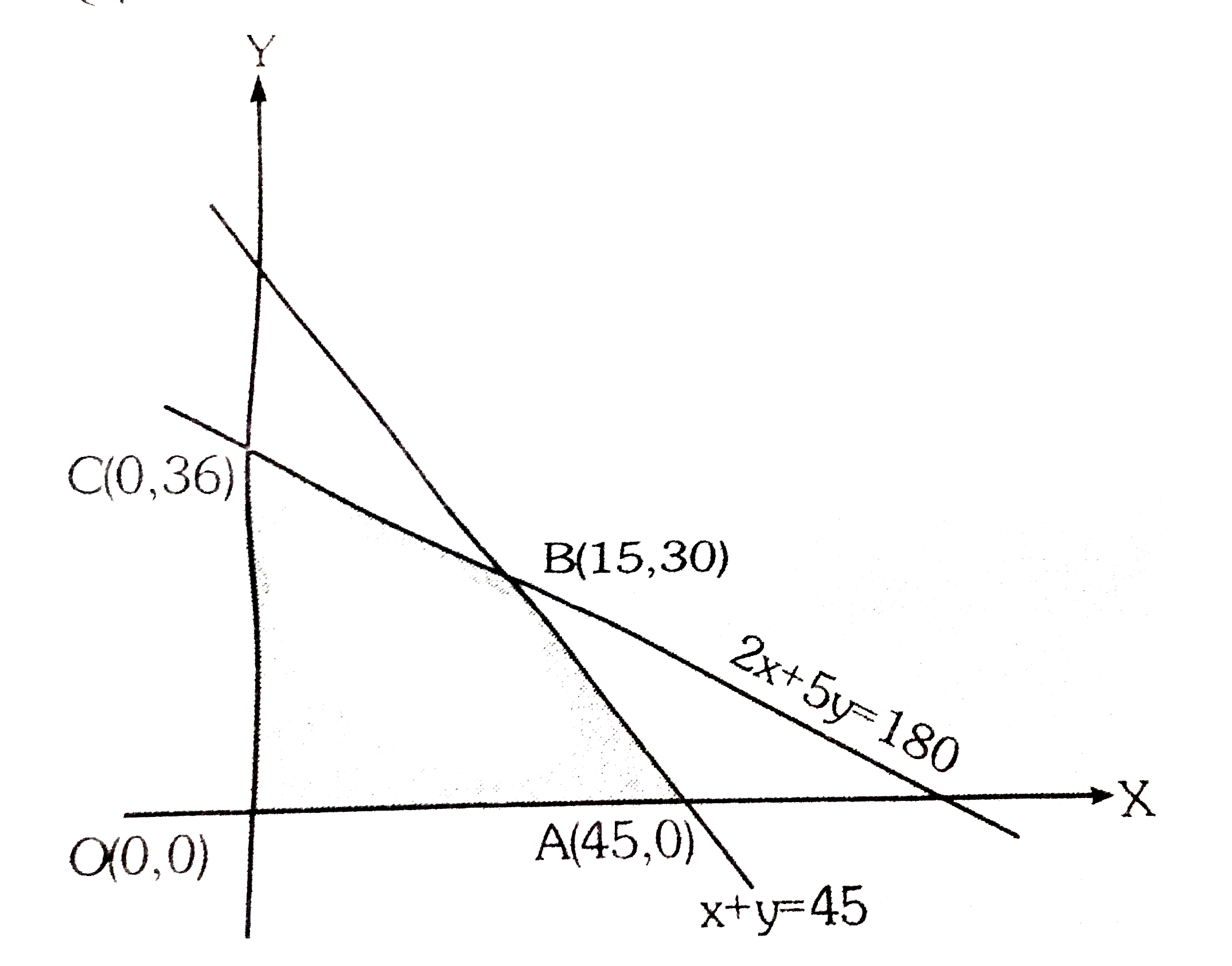 चूँकि शीर्ष B(15,30) पर उद्देश्य फलन का मान अधिकतम 1,20,000 हैं । अतः शीर्ष B इष्टतम हल का बिंदु हैं । अतः वाहन निर्माता को अधिकतम लाभ के लिए 15 मोटर कार तथा 30 ट्रक बनाना चाहिए जिस पर उसको अधिकतम लाभ = 1,20,000 रुपये होगा ।
चूँकि शीर्ष B(15,30) पर उद्देश्य फलन का मान अधिकतम 1,20,000 हैं । अतः शीर्ष B इष्टतम हल का बिंदु हैं । अतः वाहन निर्माता को अधिकतम लाभ के लिए 15 मोटर कार तथा 30 ट्रक बनाना चाहिए जिस पर उसको अधिकतम लाभ = 1,20,000 रुपये होगा ।
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - बहुविकल्पीय प्रश्न
13 Videos
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास प्रश्न 23.1
8 Videos
- प्रायिकता क्रमश:BOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकता क्रमश:EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.3
7 Videos
Similar Questions
रैखिक प्रोग्रामन समस्या निम्न व्यवरोधों के अन्तर्गत x1+2x2≤2000,x1+x2≤1500,x2≤600 और x1,x2≥0 हैं तो कौन - सा बिंदु घिरा हुए धन भाग में नही हैं ?
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
3x1+2x2≤12
5x1≤1
x1+x2≥8
−x1+x2≥4
तथा x1,x2≥0
अधिकतम z=x1+12x2
View Solutionएक प्रश्न-पुस्तिका में 300 सरल सत्य/असत्य प्रश्न, 200 कठिन सत्य/असत्य प्रश्न, 500 सरल बहुविकल्पीय प्रश्न तथा 400 कठिन बहुविकल्पीय प्रश्न है | यदि प्रश्न-पुस्तिका से एक प्रश्न का चयन यदृच्छया किया जाता है | सिद्ध कीजिए कि इस प्रश्न के सरल होने की प्रायिकता 59 है जबकि यह एक बहुविकल्पीय प्रश्न है |
View Solutionवास्तविक संख्याओं के समुछ्य R में प्राचित्रण f(x)=sinx,x∈R तथा g(x)=x2,x∈R द्वारा परिभाषित है सिद्ध कीजिय की gof≠fog
View Solutionआपके पिताजी अपनी पुरानी कार बेचना चाहते हैं। इसके लिए पूरा विवरण देते हुए एक विज्ञापन का आलेख लगभग 50 शब्दों में तैयार कीजिए।
View Solutionआप अपने विद्यालय में सांस्कृतिक सचिव हैं। विद्यालय में होने वाली कविता-प्रतियोगिता में भाग लेने के लिए आमंत्रण हेतु 25-30 शब्दों में एक सूचना तैयार कीजिए।
View Solutionआप एक अच्छे चित्रकार हैं। अपने चित्रों की प्रदर्शनी के लिए लगभग 50 शब्दों में एक विज्ञापन तैयार कीजिए।
View Solutionऊँट तथा कैक्टस निम्नलिखित में किस प्रकार के वासस्थान के लिए अनुकूलित हैं?
View Solutionटी० बी० चैनलों में तत्काल प्रसारित समाचारों के प्रकारों में से एक हैं
View Solutionभाषा शिक्षक के रूप में आपके लिए महत्वपूर्ण है
View Solutionवे शब्द जो धातु या शब्द के अंत में जोड़े जाते हैं उन्हें काया कहते हैं ?
View SolutionWhich one of the following is not a digestive enzyme in the human system? मानव तन्त्र में निम्नलिखित में से कौन-सा एक पाचक एन्जाइम नहीं हैं ?
View Solutionएक परमाणु में, दो इलेक्ट्रॉन नाभिक के चारों त्रिज्या r और 4r की वृत्ताकार कक्षाओं में परिक्रमण करते हैं। एक परिक्रमण को पूर्ण करने के लिए उनके द्वारा लिए गए समय का अनुपात (T_2 : T_1) है:
View Solutionनायलॉनप 6,6 के एकलकों में से एक, एक अम्ल है। इस अम्लीय एकलक में कितने -COOH समूह उपस्थित हैं?
View Solution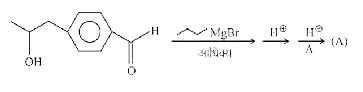
उपरोक्त अभिक्रिया में (A) के लिए कितने ज्यामितीय समावयवी संभव हैं?
View Solutionसुक्रोस के एक अणु में कितने –OH समूह उपस्थित हैं?
View Solution
