एक अवकाश प्राप्त व्यक्ति 70,000 रुपये निवेश कर सकता हैं तथा दो प्रकार के बॉण्ड बाजार में हैं । प्रथम बॉण्ड में निवेश की गयी धनराशि का 8 तथा दूसरे बॉण्ड में निवेश की गयी धनराशि का 10 वार्षिक मिलता हैं । उपरोक्त के अनुसार वह कम से कम 10000रुपये पहले बॉण्ड में तथा दूसरे बॉण्ड में 30,000 अधिक निवेश नहीं कर सकता हैं । एक वर्ष बाद अधिकतम रिटर्न के लिए वह किस प्रकार निवेश करेगा ?
माना वह बॉण्ड A में Rs. x तथा बॉण्ड B में Rs. y निवेश करता हैं ।
∴ इसे निम्न समीकरण व्दारा व्यक्त करेंगे -
z=8x100+10y100
⇒z=0.08x+0.1y
x + y = 70,000
x≥10000
y≤30000
x+y=70000
⇒x70000+y70000=1
अतः (0,0) , x+y≤70000 को संतुष्ट करता हैं । इससे निष्कर्ष निकलता हैं कि
(i) AB के नीचे क्षेत्र x+y≤70000
(ii) x≥10000 वह क्षेत्र है जो y-अक्ष के समान्तर है तथा इसके दायीं ओर तथा रेखा x = 10000 से दूर हैं इसलिए रेखा के दायीं ओर का क्षेत्र x≥=10000 को प्रदर्शित करता हैं ।
(iii) y≤30000 वह क्षेत्र है जो x-अक्ष के समान्तर हैं तथा उसके ऊपर हैं परंतु रेखा y = 30,000 से नीचे हैं । इसलिए रेखा EF नीचे , x-अक्ष का क्षेत्र y≤30000 को प्रदर्शित करता हैं ।
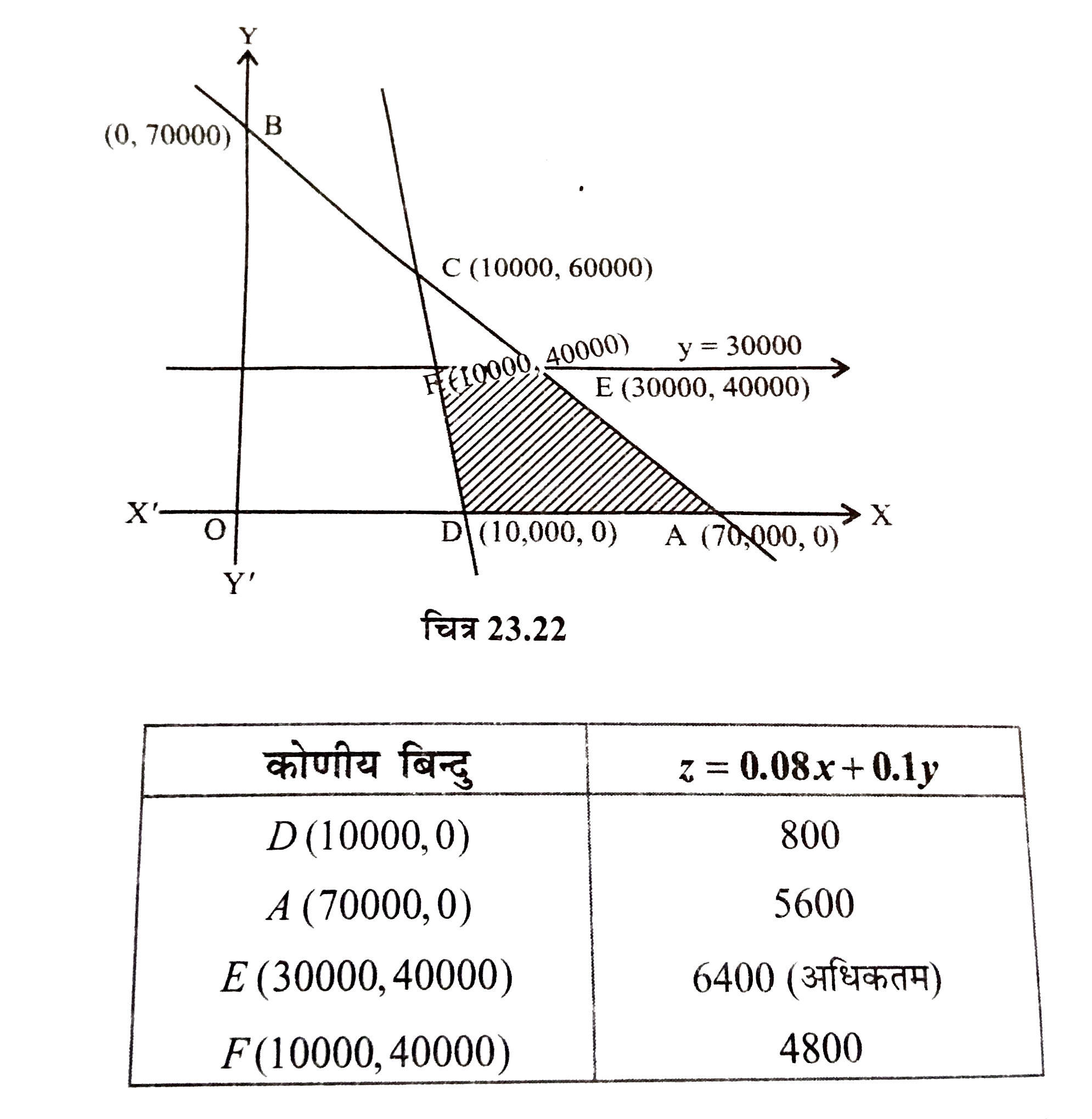
स्पष्टतः बिंदु E(30000, 40000) पर z का अधिकतम मान 6400 हैं । इसलिए अधिकतम वार्षिक रिटर्न के लिए उसे बॉण्ड A में Rs.30000 तथा B बॉण्ड B में Rs.40000 निवेश करने होंगे ।
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - बहुविकल्पीय प्रश्न
13 Videos
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास प्रश्न 23.1
8 Videos
- प्रायिकता क्रमश:BOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकता क्रमश:EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.3
7 Videos
Similar Questions
रैखिक प्रोग्रामन समस्या निम्न व्यवरोधों के अन्तर्गत x1+2x2≤2000,x1+x2≤1500,x2≤600 और x1,x2≥0 हैं तो कौन - सा बिंदु घिरा हुए धन भाग में नही हैं ?
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
3x1+2x2≤12
5x1≤1
x1+x2≥8
−x1+x2≥4
तथा x1,x2≥0
अधिकतम z=x1+12x2
View Solutionएक प्रश्न-पुस्तिका में 300 सरल सत्य/असत्य प्रश्न, 200 कठिन सत्य/असत्य प्रश्न, 500 सरल बहुविकल्पीय प्रश्न तथा 400 कठिन बहुविकल्पीय प्रश्न है | यदि प्रश्न-पुस्तिका से एक प्रश्न का चयन यदृच्छया किया जाता है | सिद्ध कीजिए कि इस प्रश्न के सरल होने की प्रायिकता 59 है जबकि यह एक बहुविकल्पीय प्रश्न है |
View Solutionवास्तविक संख्याओं के समुछ्य R में प्राचित्रण f(x)=sinx,x∈R तथा g(x)=x2,x∈R द्वारा परिभाषित है सिद्ध कीजिय की gof≠fog
View Solutionनिम्नलिखित प्रश्नों में से किसी एक प्रश्न का उत्तर लगभग 90 शब्दों में लिखिए कवि बैरागी माँ से किस प्रकार के वरदान की अपेक्षा रखते हैं
View Solutionयदि समुच्चय A में 5 अवयव हैं तथा समुच्चय B में 6 अवयव हैं , तो A से B में एकैकी तथा आच्छादक प्रतिचित्रणों कि संख्या हैं :
View Solutionपृथ्वी तथा भारत में कितनी जातियां हैं ?
View Solutionऊँट तथा कैक्टस निम्नलिखित में किस प्रकार के वासस्थान के लिए अनुकूलित हैं?
View Solutionपृथ्वी तथा भारत में कितनी जातियां हैं ?
View SolutionA and B invest in the ratio 3:5. After 6 months, C joins the business, investing an amount equal to B's. At the end of the year what will be the ratio of their profits? A और B 3:5 के अनुपात में निवेश करते है। 6 महीने के बाद, C व्यवसाय में शामिल हो जाता है तथा B के बराबर राशि का निवेश करता है। वर्ष के अंत में उनके लाभ का अनुपात क्या होगा?
View Solutionभारत में फाइलें एक विभाग से दूसरे विभाग में पहुँचती हैं यह किरा विडम्बना की ओर संकेत करता है?
View Solutionमेरे घर में पाँच जोड़ी आँखें हैं माँ की आँखें पड़ाव से पहले ही तीर्थ यात्रा की बस के दो पंचर पहिए हैं। पिता की आँखें लोहसाँय की ठंडी शलाखें हैं बेटी की आँखें मंदिर में दीवट पर ' जलते घी के दो दिए हैं। कविता के अनुसार मेरे घर में कितनी जोड़ी आँखें हैं ?
View SolutionThe ratio of investment by A to that by B is a business is 14:15 and the ratio of their respective profits at the end of a year is 2:5. If A invested the money for 3 months, then for how much time (in months) B invested his money?
एक व्यवसाय में A और B के द्वारा किये गए निवेश का अनुपात 14:15 है तथा वर्ष के अंत में उनके लाभों का अनुपात 2 : 5 है | यदि A ने 3 माह के लिए राशि निवेश की थी, तो B द्वारा निवेश की गयी राशि की अवधि (महीने में ) कितनी थी ?
View SolutionA, B and C started a business. Thrice the investment of A is equal to twice the investment of B and also equal to four times the investment of C. If C’s share out of the total profit is Rs. 4,863,then the share of A in the profit is:
A, B और C ने एक व्यवसाय की शुरुआत की | A के निवेश का तिगुना B के निवेश के दोगुने तथा C के निवेश के चार गुना के बराबर है | यदि कुल लाभ में C का हिस्सा 4863 रुपये है, तो इस लाभ में A का हिस्सा ज्ञात करें |
View SolutionA,B and C start a business. A invests 3313% of the total capital, B invests 25% of the remaining and C invests the rest.If the total profit at the end of a year is Rs. 1,62,000, then A’s share in profit is :
A,B और C ने एक व्यवसाय की शुरुआत की | A ने कुल पूँजी का 33 13% निवेश किया |B ने शेष का 25% निवेश किया तथा शेष राशि C के द्वारा निवेश की गयी | यदि वर्ष के अंत में कुल लाभ 1, 62, 000 रुपये है, तो इस लाभ में A का हिस्सा है :
View Solutionकिसी परीक्षा में एक छात्र को 40% अंक प्राप्त होते हैं तथा वह 20 अंकों से असफल हो जाता है। उसी परीक्षा में दूसरे ,छात्र को 45% 'अंक प्राप्त होते हैं, तथा उसके प्राप्त अंक पास होने के लिए न्यूनतम अंक से 5 अधिक है। परीक्षा का पूर्णांक ज्ञात कीजिए।
View Solution
