एक उत्पादक दो प्रकार के उत्पाद A तथा B का निर्माण करता हैं । दोनों उथ्पादों को दो विभिन्न मशीनों की आवश्यकता होती हैं । पहली मशीन की उपलब्ध क्षमता 12 घण्टे/दिन तथा दूसरी मशीन की 9 घण्टे/दिन हैं ।
उत्पाद A की प्रत्येक इकाई को दोनों मशीनों पर 3 घण्टों की आवश्यकता है तथा उत्पाद B की प्रत्येक इकाई को पहली मशीन पर 2 घण्टों तथा दूसरी मशीन पर 1 घण्टे की आवश्यकता है । उत्पाद A की प्रत्येक इकाई 7 रुपये के लाभ तथा B की 4 रुपये के लाभ पर बेची जाती हैं । आलेखनीय विधइ व्दारा अधिकतम लाभ के लिए उत्पादन स्तर प्रति दिन ज्ञात कीजिए ।
माना उत्पादक उत्पाद A तथा B के क्रमशः x तथा y इकाई का निर्माण करता हैं ।
हम निम्नलिखित सारणी बनाते हैं -
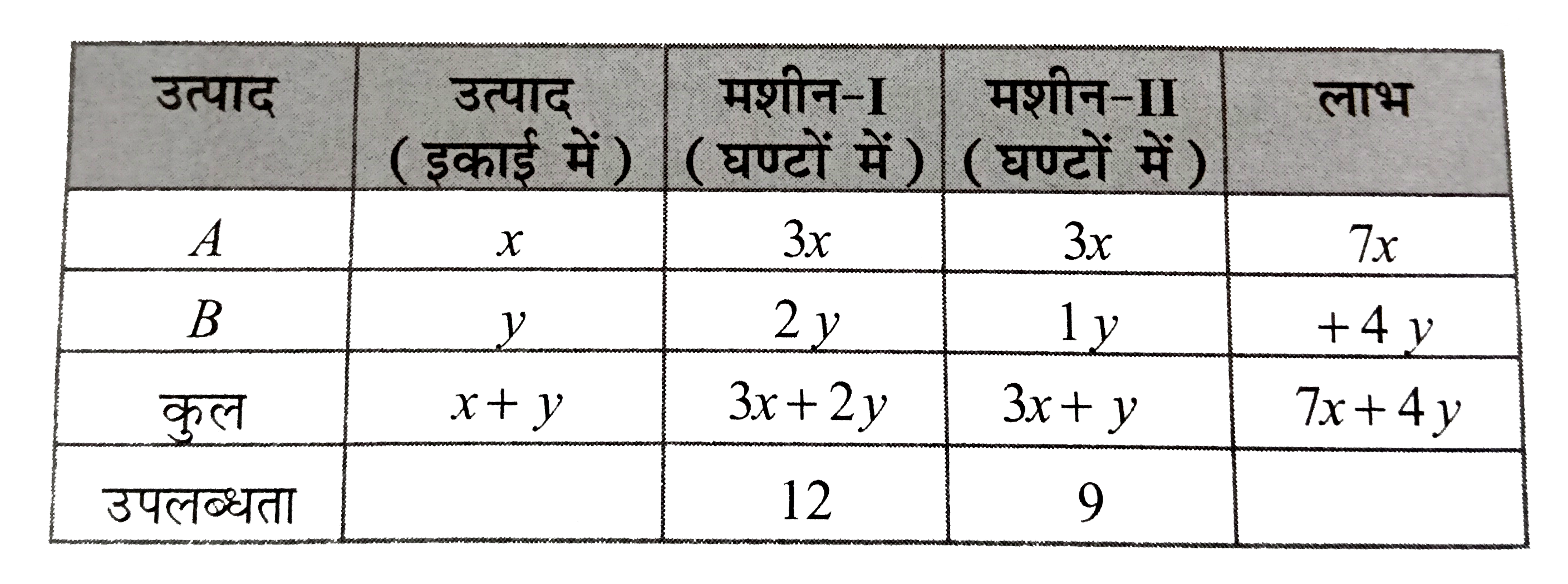
कुल लाभ , z = 7x + 4y ...(1)
z = 7x + 4y का निम्नलिखित व्यवरोधों के निकाय ,
3x+2y≤12
3x+y≤9
तथा x≥0,y≥0 के अन्तर्गत अधिकतमीकरण करों । अब, दी गई असमिकाओं को समीकरण बनाने पर -
3x + 2y = 12 ...(2)
3x+y=9 ...(3)
3x+2y=12 या y=12−3x2 के लिए सारणी हैं -

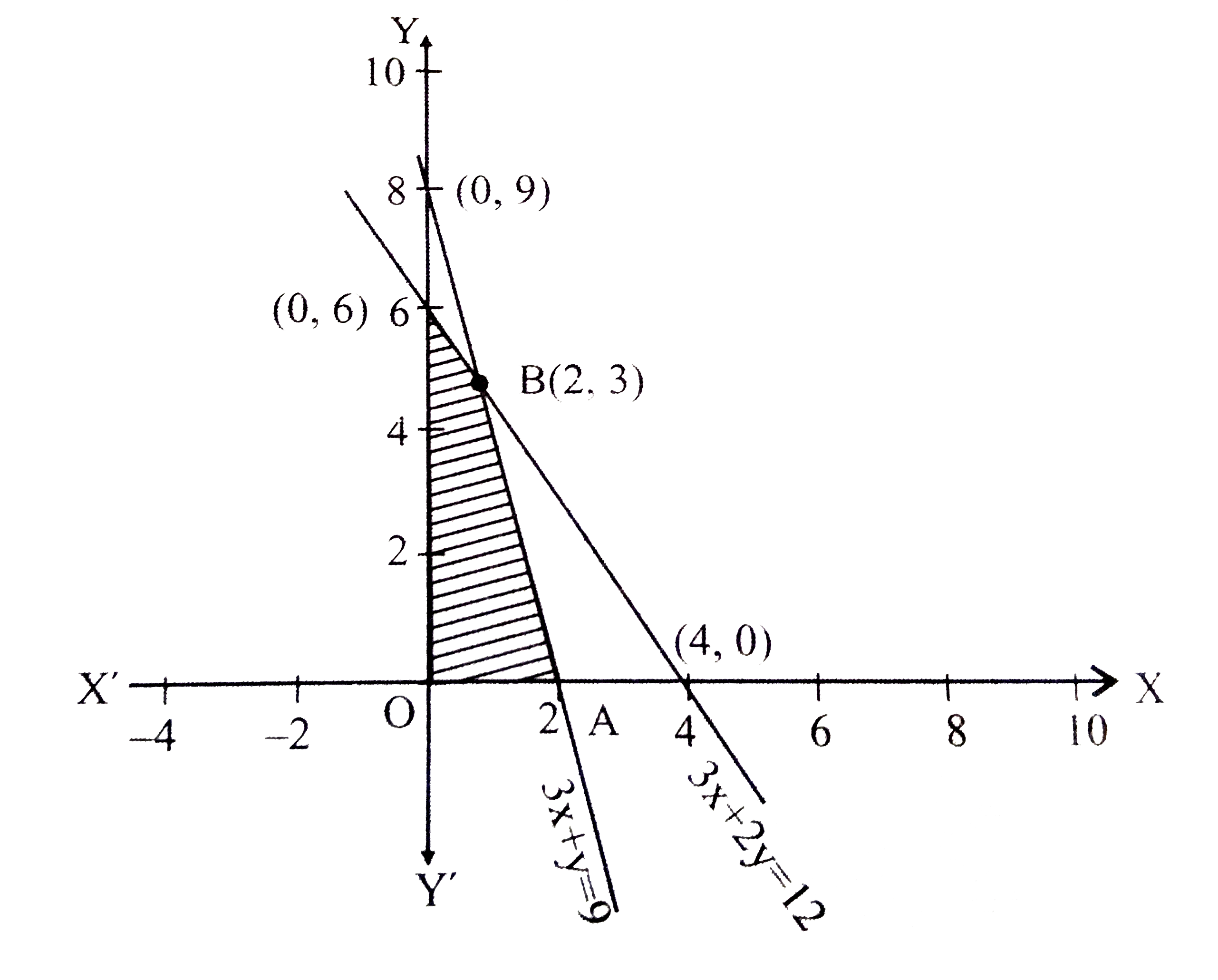
यह बिंदुओं (0,6) तथा (4,0) से होकर गुजरती हैं ।
असमिका 3x+2y≤12 में (0,0) रखने पर -
0+0≤12
⇒0≤12 (सत्य)
अतः अर्ध्दतल मूलबिंदु की ओर हैं ।
रेखा 3x + y = 9 या y = 9 - 3x के लिए सारणी -

यह बिंदुओं (0,9) तथा (3,0) से होकर गुजरती हैं ।
असमिका 3x+y≤9 में (0,0) रखने पर -
0+0≤9
⇒0≤9 (सत्य)
अतः अर्ध्दतल मूल बिंदु की ओर हैं ।
x≥0 तथा y≥0 , अतः क्षेत्र पहले चतुर्थांश में अब , रेखा (1) तथा (2) के प्रतिच्छेदन बिंदु हैं -
(3x + 2y) - (3x + y ) = 12 - 9
⇒ y = 13
तथा 3x=12−2×3
⇒ 3x = 12 - 6 ⇒ x = 2 अतएव , प्रतिच्छेदन बिंदु (2,3) हैं ।
असमिकाओं का आलेख निम्न हैं -
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - बहुविकल्पीय प्रश्न
13 Videos
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास प्रश्न 23.1
8 Videos
- प्रायिकता क्रमश:BOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकता क्रमश:EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.3
7 Videos
Similar Questions
रैखिक प्रोग्रामन समस्या निम्न व्यवरोधों के अन्तर्गत x1+2x2≤2000,x1+x2≤1500,x2≤600 और x1,x2≥0 हैं तो कौन - सा बिंदु घिरा हुए धन भाग में नही हैं ?
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
3x1+2x2≤12
5x1≤1
x1+x2≥8
−x1+x2≥4
तथा x1,x2≥0
अधिकतम z=x1+12x2
View Solutionएक प्रश्न-पुस्तिका में 300 सरल सत्य/असत्य प्रश्न, 200 कठिन सत्य/असत्य प्रश्न, 500 सरल बहुविकल्पीय प्रश्न तथा 400 कठिन बहुविकल्पीय प्रश्न है | यदि प्रश्न-पुस्तिका से एक प्रश्न का चयन यदृच्छया किया जाता है | सिद्ध कीजिए कि इस प्रश्न के सरल होने की प्रायिकता 59 है जबकि यह एक बहुविकल्पीय प्रश्न है |
View Solutionवास्तविक संख्याओं के समुछ्य R में प्राचित्रण f(x)=sinx,x∈R तथा g(x)=x2,x∈R द्वारा परिभाषित है सिद्ध कीजिय की gof≠fog
View Solutionएक फैक्टरी दो पदार्थो A और B का निर्माण करती है|पदार्थ A के निर्माण हेतु एक मशीन को 1 .5 घंटे तथा साथ ही एक मिस्त्री को 2 घंटे कार्य करना पढता है|पदार्थ B के निर्माण हेतु मशीन को 2 .5 घंटे तथा मिस्त्री को 1 .5 घण्टे कार्य करना पढता है| प्रति सप्ताह फैक्टरी मशीन को 80 घंटे तथा कारीगरी को 70 घंटे उपलब्ध करात्ती है| प्रत्येक पदार्थ A पर लाभ रु 5 तथा प्रत्येक पदार्थ B पर लाभ रु 4 है| यदि निर्मित सभी पदार्थ बिक जाएँ तो ज्ञात कीजिए की प्रति सप्ताह अधिकतम लाभ के लिए प्रत्येक प्रकार के कितने पदार्थ बनाये जाएँ ?
View Solutionएक कारखाने में दो प्रकार के पेंच A और B बनते है|प्रत्येक के निर्माण मै दो मशीनों के प्रयोग की आवश्यकता होती है, जिसमें एक स्वचालित और दूसरी हस्तचलित है| एक पैकेट पेंच A के निर्माण में 4 मिनट स्वचालित और 6 मिनट हस्तचालित मशीन तथा एक पैकेट पेंच B के निर्माण में 6 मिनट स्वचालित तथा 3 मिनट हस्तचालित मशीन पर कार्य होता है| प्रत्येक मशीन किसी भी दिन के लिए अधिकतम 4 घंटे काम के लिए उपलब्ध है|निर्माता पेंच A के प्रत्येक पैकेट 70 पैसे और पेंच B के प्रत्येक पैकेट पर रु 1 का लाभ कमाता है| यह मानते हुए की कारखाने में निर्मित सभी पेचों के पैकेट बिक जाते है, ज्ञात कीजिए की लाभ कमाता है| यह मानते हुए की कारखाने में निर्मित सभी पेंचो के पैकेट बिक जाते है| तथा ज्ञात कीजिए की प्रतिदिन कितने मालिक द्वारा कितने पैकेट विभिन्न पेंचो के बनाये जाएँ जिससे लाभ अधिकतम हो| उपयुक्त रैखिक प्रोग्रामन समस्या को सूत्रबद्ध कीजिए तथा इसे ग्राफ़िये विधि से हल कीजिए तथा अधिकतम लाभ ज्ञात कीजिए|
View Solution5 लड़कियों तथा 7 लड़कों की एक कक्षा का विचार कीजिए। इस कक्षा की 2 लड़कियों तथा 3 लड़कों को लेकर बन सकने वाली भिन्न टीमों यदि दो विशेष लड़के A तथा B एक ही टीम के सदस्य बनने से मना करते हैं , की संख्या है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionहैलोऐल्केन तथा हैलोऐरीन को बनाने की विधि
View Solutionसजीवों को ऊर्जा के लिए .....तथा श्वसन की आवश्यकता होती है।
View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
View Solutionसजीवों को भोजन की आवश्यकता क्यों होती है ?|भोजन की पूर्ती |फसल |फसल उत्पादन की आवश्यकता क्यों ?|फसलों के प्रकार |Summary
View Solutionएक बस 3 घण्टे में 126 किमीo तथा एक ट्रेन 5 घण्टे में 315km दूरी तय करते है। बस तथा ट्रेन की चालों का अनुपात ज्ञात करो।
View Solution9 व्यक्ति किसी काम को 5 दिन में करते हैं। यदि इस काम को 3 दिनों में खत्म करना है तब कितने व्यक्तियों की अतिरिक्त आवश्यकता होगी
View SolutionTwo articles are sold for Rs.9,720 each. On one, the seller gains 8% and on the other, he loses 10%. What is his overall gain or loss?
दो वस्तुएँ 9720 रुपये में एक की दर से बेची जाती हैं | पहली वस्तु पर, विक्रेता को 8% का लाभ होता है तथा दूसरी पर उसे 10% की हानि होती है | उसका कुल लाभ या हानि क्या है ?
View SolutionTwo articles are sold for Rs. 5,104 each. On one, the seller gains 16% and on the other, he loses 12%. What is his overall gain percent, nearest to two decimal places?
दो वस्तुएँ 5104 रुपये में एक की दर से बेची जाती हैं | पहली वस्तु पर विक्रेता को 16% लाभ होता है तथा दूसरी पर उसे 12% की हानि होती है | दो दशमलव स्थानों तक उसका कुल लाभ प्रतिशत ज्ञात करें |
View Solution
