20 मी, 34 मी और 42 मी भुजाओ वाले एक त्रिभुजाकार मैदान के तीन कोणों पर तीन घोड़े 7 मी लम्बी रस्सी से बाँध दिए गए है ज्ञात कीजिए कि मैदान के कितने क्षेत्र को घोड़ो द्वारा चरा जा सकता है और यह भी ज्ञात कीजिए कि मैदान का कितना भाग बिना चरे बचेगा ?
259m2
160m2
150m2
100m2
The correct Answer is:A
माना कि A, B तथा C के कोण क्रमशः θ1,θ2 तथा θ3 है
चूँकि घोड़ो द्वारा चारे योग्य क्षेत्र का क्षेत्रफल = तीन त्रिज्यखंडो जिनके केंद्रीय कोण θ1,θ2 और θ3 है और प्रत्येक की त्रिज्या 7 मी है के क्षेत्रफलों का योग
=(πr2θ1360∘+πr2θ2360∘+πr2θ3360∘)मी2
=πr2360∘(θ1+θ2+θ3)(πr2×180∘360∘)
=(227×7×712)=77मी2
दिया है त्रिभुज की भुजाएं a=20 मी, b=34 मी तथा c=42 मी
इसलिए s=12(a+b+c)=48 मी, (s-a)=28 मी, (s-b)=14 मी तथा (s-c)=6 मी
अब पूरे मैदान का क्षेत्रफल =ΔABC का क्षेत्रफल
=√x(s−1)(s−b)(s−c)=√48×28×14×6=334मी2
अतः बिना चारे जाने वाले मैदान का क्षेत्रफल =ΔABC का क्षेo तीन कोणों के तीन त्रिजयखंडो के क्षेo का योग
=(336−77)मी2=259 मी2

Topper's Solved these Questions
- वृत्तों से समबन्धित क्षेत्रफल BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - अभ्यास प्रश्न 12.1
10 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - BALAJI PUBLICATIONCHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - अभ्यास प्रश्न 12.2
10 Videos
- वृत्त BOOK - BALAJI PUBLICATIONCHAPTER - वृत्त EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- समांतर श्रेणीBOOK - BALAJI PUBLICATIONCHAPTER - समांतर श्रेणीEXERCISE - स्वमूल्यांकन परीक्षण
22 Videos
Similar Questions
एक वृत्त की त्रिज्या 8.4 सेमी है वृत्त की परिधि तथा क्षेत्रफल ज्ञात कीजिए
View Solution21 सेमी त्रिज्या वाले एक वृत्त से एक त्रिज्यखण्ड काटा जाता है त्रिज्यखण्ड का कोण 150∘ है चाप की लम्बाई तथा क्षेत्रफल ज्ञात कीजिए ।
View Solutionदिये गये चित्र में TAB, O केंद्र वाले वृत्त की छेदक रेखा है तथा वृत्त के बिन्दु P पर TP एक स्पर्शी है। यदि TP = 5.6 सेमी तथा TA = 2.8 सेमी हो तब जीवा AB की माप ज्ञात कीजिए ।
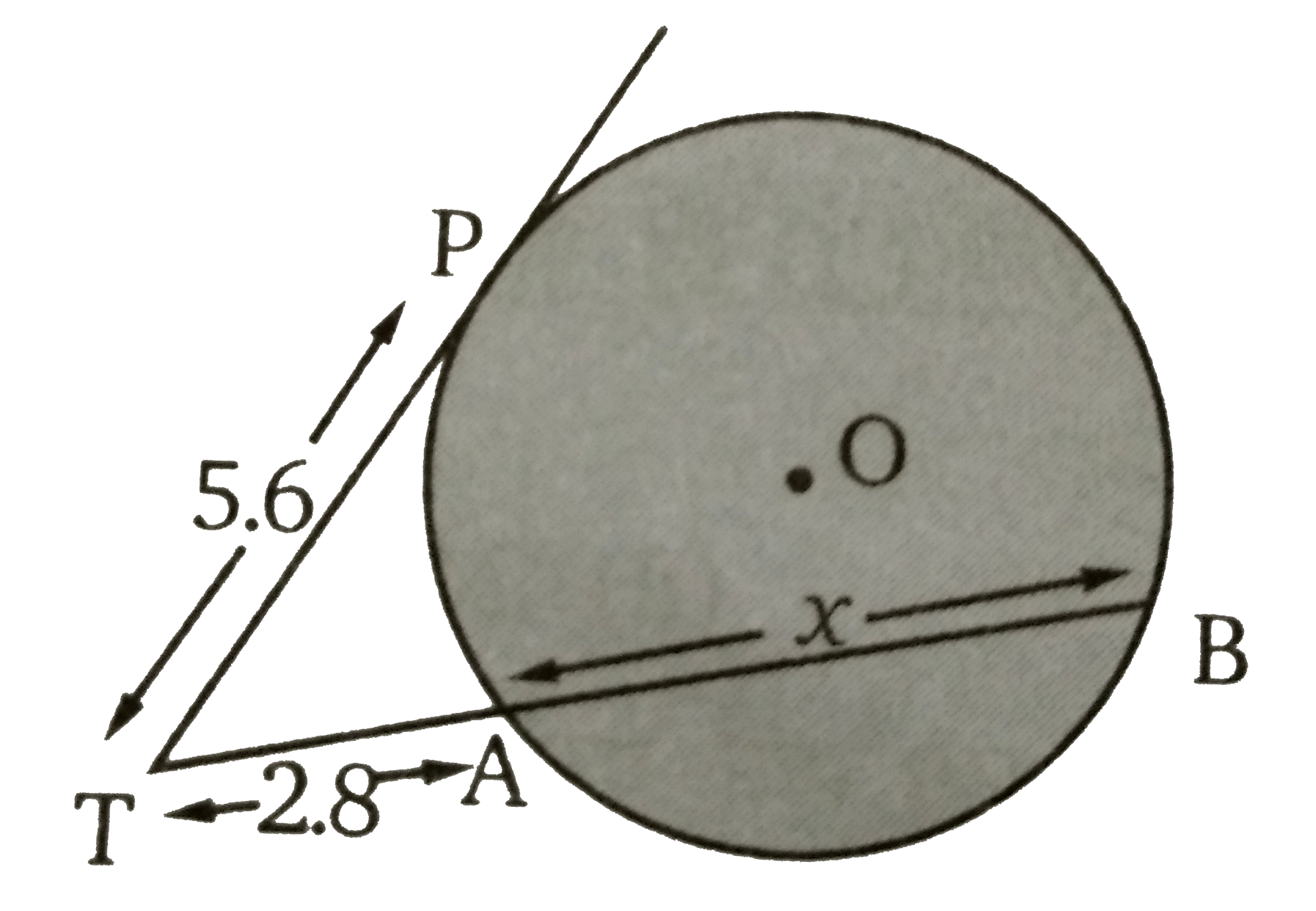
View Solutionसिद्ध कीजिए कि निम्न स्थिति एक समांतरर श्रेणी बनाती है। एक दीवार को पहले एक मीटर बनाने का खर्च रू0 150 तथा प्रत्येक आनेवाले मीटर में रू0 20 का खर्च बढ़ता है।
View Solutionपृथ्वी की त्रिज्या 6.4×106 मी है। पृथ्वी-तल से 800 किमी की ऊँचाई पर गुरुत्वीय विभव तथा गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए। (g=10 मी/से.2)
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionउस दीर्घवृत का समीकरण ज्ञात कीजिए जो बिन्दुओ (−3,1) और (2,−2) से होकर जाता है तथा जिसका केंद्र मूलबिंदु पर है । उत्केंद्रता भी ज्ञात कीजिए ।
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक रेखा बिंदु 2ˆi+ˆj−3ˆk से गुजरती है और साधीश ˆi+2ˆj+ˆk के समांतर है । रेखा का सदिश समाकरण ज्ञात कीजिए। इसके द्वारा रेखा का कार्तीय समीकरण ज्ञात कीजिए।
View Solutionएक दंपत्ति के दो बच्चे है। प्रायिकता ज्ञात कीजिए
दोनों बच्चें लड़कियाँ है , यदि यह ज्ञात है कि बड़ा बच्चा लड़का है।
View Solutionकिसी बेलन का अर्धव्यास 2 मी/से की दर से बढ़ता है और ऊँचाई 3 मी/से की दर से घटती है। जब उसकी ऊँचाई 5 मी और अर्धव्यास 3 मी हो, तो बेलन के आयतन के परिवर्तन की दर होगी
View Solutionएक धातु के बेलन को, जिसका व्यास 8 से.मी. और ऊँचाई 90 से. मी. है, गलाकर 12 से. मी. व्यास वाले कितने गोले बनाए जा सकते हैं ?
View Solutionनीचे दिए गए गद्यांश को पढ़कर पूछे गए प्रश्नों के सही/सबसे उचित उत्तर वाले विकल्प को चुनिए।
शिक्षा आज दुविधा के अजब दोराहे पर खड़ी है। एक रास्ता चकाचौंध का है, मृगतृष्णा का है। बाजार की मृगतृष्णा शिक्षार्थी को लोभ-लालच देकर अपनी तरफ दौड़ाते रहने को विवश करने को उतारू खड़ी है। बाजार के इन ललचाने वाले रास्तों पर आकर्षण है, चकाचौंध है और सम्मोहित कर देने वाले सपने है। दूसरी तरफ शिक्षा का साधना मार्ग है, जो शान्ति दे सकता है, सन्तोष दे सकता है और हमारे आत्मतत्व को प्रबल करता हुआ विमल विवेक दे सकता है। निश्चित ही वह मार्ग श्रेयस्कर है, मगर अपनी ओर आकर्षित करने वाले आजार का मार्ग प्रेयस्कर है। इस दोराहे पर खड़ा शिक्षार्थी बाजार को चुन लेता है। लाखों-करोड़ों लोग आज इसी रास्ते के लालच में आ गए हैं और शिक्षा के भंवरजाल में फंस गए हैं। बाजार की खूबी यही है कि वह फंसने का अहसास किसी को नहीं होने देता और मनुष्य लगातार फैसता चला जाता है। किसी को यह महसूस नहीं होता कि वह दलदल में है, बल्कि महसूस यह होता है कि बाजार द्वारा दिए गए पैकेज के कारण वह सुखी है। अब यह अलग बात है कि सच्चा सुख क्या है? और सुख का भ्रम क्या है? जरूरत विचार करने की है। सवाल यह है कि बाजार विचार करने का भी अवकाश देता है या कि नहीं।
गद्यांश के आधार पर कहा जा सकता है कि
View Solution
