Question

एक समकोण त्रिभुज, जिसकी भुजाऐं 3 सेमी और 4 सेमी हैं । ( कर्ण के अतिरिक्त ) को उसके कर्ण के परित घुमाया जाता है । इस प्रकार प्राप्त द्वि-शंकु के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।

Explanation

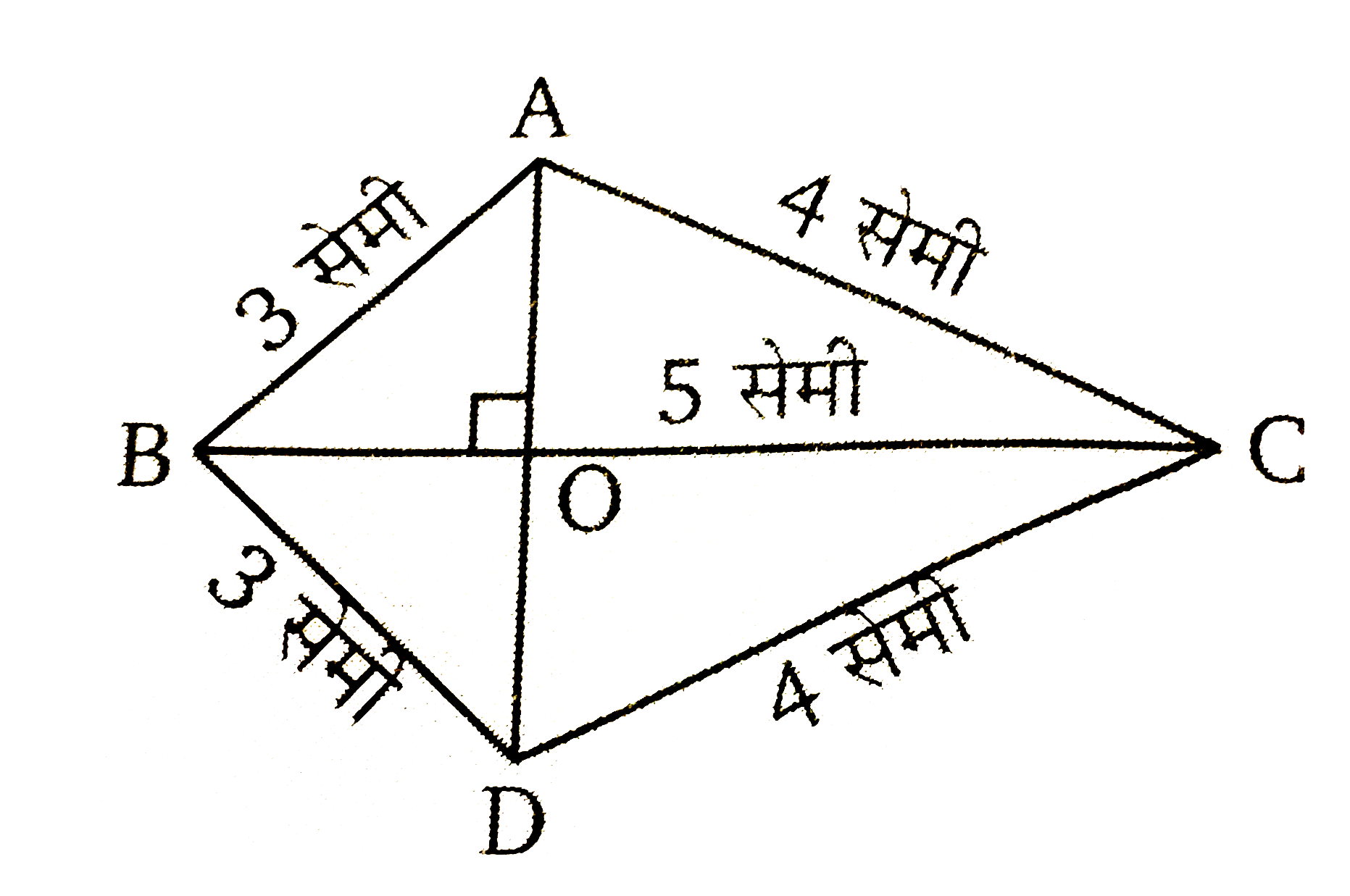
चित्र द्वारा, `BC=sqrt(3^(2)+4^(2))=5` सेमी
स्पष्ट है कि `AO=DO,BC` के परितः समकोण त्रिभुज को घुमाने पर प्राप्त द्वि-शंकु के उभयनिष्ठ आधारों की त्रिज्या है ।
अब, शंकु BAD की ऊँचाई `=BO`
शंकु की तिर्यक ऊँचाई `=3` सेमी
शंकु CAD की ऊँचाई `=CO`
शंकु की तिर्यक ऊँचाई `=4` सेमी
तब, AA-समरूपता द्वारा,
`DeltaAOB~~DeltaCAB`
`rArr (AO)/(CA)=(AB)/(CB)`
`rArr (AO)/(4)=3/5 rArr AO=2.4` सेमी
अतः `(OB)/(CA)=(AB)/(CB)rArr(OB)/(3)=3/5 rArr OB=1.8` सेमी
तथा `OC=BC-OB`
`=5-1.8` सेमी `=3.2`सेमी
द्वि-शंकु का आयतन `=`शंकु ABD का आयतन + शंकु ACD का आयतन
`=1/3 pi r^(2) (OB+OC)`
`=[1/3xx22/7xx2.4xx2.4xx(1.8+3.2)]=30.17 "सेमी"^(3)`
तथा द्वि-शंकु का पृष्ठीय क्षेत्रफल `=pi r (AB+AC)`
`=22/7xx2.4xx(3+4)=52.8 "सेमी"^(2)`