लकड़ी का एक खिलौना रॉकेट एक शंकु के आकार का है , जो एक बेलन पर अध्यारोपित है जैसा कि आकृति में दर्शाया गया है । सम्पूर्ण रॉकेट की ऊँचाई 26 सेमी है , जबकि शंक्वाकार भाग की ऊँचाई 6 सेमी है, शंक्वाकार भाग के आधार का व्यास 5 सेमी और बेलनाकार भाग का व्यास 3 सेमी है यदि शंक्वाकार भाग पर नारंगी रंग किया जाना है और बेलनाकार भाग का पीला रंग किया जाना है, तो प्रत्येक रंग द्वारा रॉकेट के रंगे जाने वाले भाग का क्षेत्रफल ज्ञात कीजिए ।
शंकु के लिए ,
त्रिज्या, r=2.5 सेमी तथा ऊँचाई, h=6 सेमी
बेलन के लिए,
त्रिज्या , r1=1.5 सेमी तथा ऊँचाई , h1=20 सेमी
यदि शंकु की तिर्यक ऊँचाई l है ।
तब l=√r2+h2=√(2.5)2+(6)2
=√6.25+36=√42.25=6.5 सेमी
स्पष्टतः नारंगी रंग से रंगे भाग का क्षेत्रफल = शंकु के वक्र पृष्ठ का क्षे० + शंकु के आधार का क्षे० - बेलन के आधार का क्षे०
=πrl+πr2−πr21=π{rl+r2−r21}
=π{2.5×6.5+(2.5)2−(1.5)2}=3.14(16.25+6.25−2.25)
=3.14×20.25=63.585सेमी2
अब पीले रंग से रंगे जाने वाले भाग का क्षे० = बेलन के वक्र पृष्ठ का क्षेत्रफल + बेलन के आधार का क्षेत्रफल
=2πr1h1+πr21=πr1(2h1+r1)
=3.14×1.5(2×20+1.5)=3.14×1.5×41.4
=4.71×41.5=195.465सेमी2
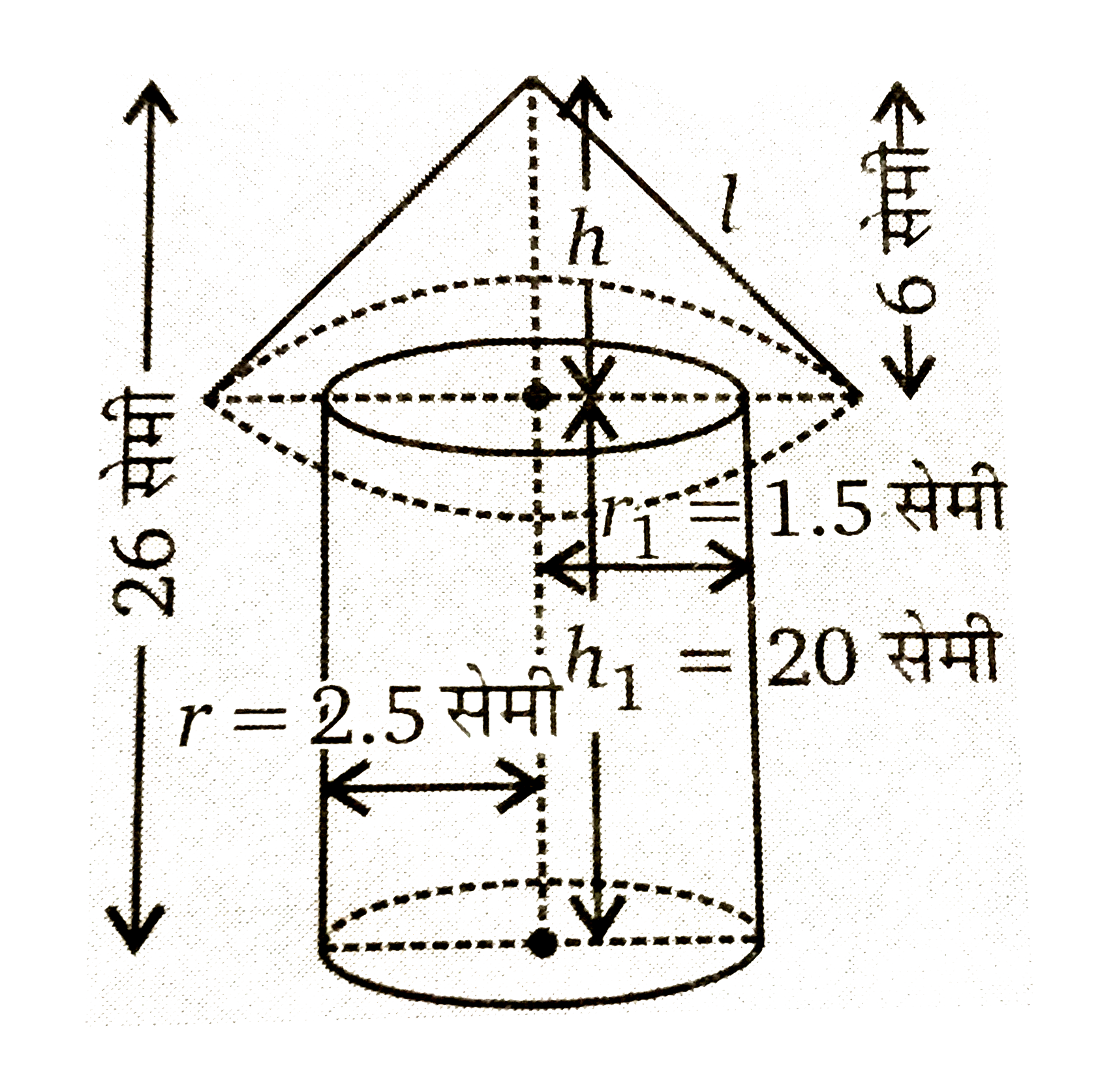
Topper's Solved these Questions
- BOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - विविध उदाहरण10videos
पृष्ठीय क्षेत्रफल और आयतन
- BOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - अभ्यास प्रश्न (13.1)24videos
पृष्ठीय क्षेत्रफल और आयतन
- BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - स्वमूल्यांकन परिक्षण26videos
निर्देशांक ज्यामिति
- BOOK - BALAJI PUBLICATIONCHAPTER - प्रश्न पत्र EXERCISE - प्रश्न89videos
प्रश्न पत्र
Similar Questions
एक घन तथा इसके ऊपर लगे एक अर्द्धगोले से एक ठोस बना है । घन की प्रत्येक भुजा का मापन 5 सेमी तथा ऊपर लगे अर्द्धगोले का व्यास 4.2 सेमी है । रंगे भाग का कुल क्षेत्रफल ज्ञात कीजिए ।
03:11View Solutionतीन घनों , जिनकी भुजाएँ क्रमशः 3 सेमी, 4 सेमी, 5 सेमी हैं, से एक घन बनायें तथा नये घन का पृष्ठीय क्षेत्रफल भी ज्ञात करें ।
02:50View Solutionसिद्ध कीजिए की बिंदु (-4 ,-1 ) ,(-2 -4 ) ,(4 ,0 ) तथा (2 ,3 ) एक आयत के शीर्ष है|
02:41View Solutionकिसी पूर्णांक m के लिए प्रत्येक धनात्मक सम पूर्णांक का रूप होगा -
02:26View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
01:18View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
02:27View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
01:49View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
02:25View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
04:30View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
02:48View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
01:44View SolutionA prism has ragular hexagonal base whose side is 12cm. The height of the prism is 24cm, it is cut into 4 equal parts by 2 perpendicular cuts as shown in figure. What is the sum of the total surface area of these four parts? एक प्रिज्म का आधार एक सम बटभुज हे जिसकी भुजा 12 सेमी. है। प्रिज्म की ऊँचाई 24 सेमी. है। इसे 2 लम्बवतकटाव द्वारा 4 बराबर भागों में काटा जाता है जैसा की चित्र में दर्शाया गया है। चारों भागों के कुल पृष्ठीय क्षेत्रफल का योग क्या है?
01:32View SolutionAssume that a drop of water is spherical and its diameter is one-tenth of a cm. A conical glass has a height equal to the diameter of its rim. If 32000 drops of water can fill the glass completely, then the height of the glass (in cm.) is मान लें कि पानी को एक बूंद गोलाकार है और इसका व्यास एक सेमी का दसवां हिस्सा है। एक शंक्वाकार गिलास की ऊँचाई, उसके आधार (rim) के व्यास के बराबर है। यूदि 32000 पानी की बूंदें गिलास को पूरी तरह से भर देती हैं, तो गिलास को ऊँचाई (सेमी में) कितना है?
View SolutionA conical cup is fined with ice-cream. The ice-cream forms a hemispherical shape on its open top. The height of the hemisphierical part is 7 cm, The radius of the hemispherical part equals to the height of the cone. Then the volume of the ice-cream is [ pi = 22/7] एक शंक्वाकार कप आइसक्रीम से भरा है। आइस्क्रोम अपने खुले शीर्ष पर अर्धगोलाकार आकृति बनाती है । अर्धगोलाकार भाग की ऊँचाई 7 सेमी है । अर्धगोलाकार भाग की त्रिज्या शंकु की ऊँचाई के बराबर हैं। आइसक्रीम का आयतन कितना होगा. ? [ pi =22/7]
View SolutionA solid is hemispherical at the bottom and conical above. If the surface areas of the two parts are equal, then the ratio of radius and height of its conical part is एक ठोस तल पर अर्द्ध गोलाकार है और ऊपर शंक्वाकार। यदि दोनों भागों के पृष्ठ क्षेत्रफल बराबर है, जो उसके शंक्वाकार भाग की त्रिज्या और ऊँचाई का अनुपात है-
02:07View SolutionBase of a right prism is an equilateral triangle of side 6 cm. If the volume of the prism is 108 sqrt3 cc. then its height is एक लंब प्रिज्म का आधार 6 सेमी. भुजा वाला समबाहु त्रिभुज है। यदि प्रिज्म का आयतन 108 sqrt3 घन सेमी. है, तो उसकी ऊँचाई है-
01:40View Solution