10 सेमी त्रिज्या वाले एक शंकु को उसके अक्ष के मध्य बिंदु से आधार के समान्तर एक तल खींचकर दो भागों में बाँटा जाता है । दोनों भागों के आयतनों की तुलना कीजिए ।
माना कि OAB एक शंकु है । जिसकी ऊँचाई OM, h है । तथा L, OM का मध्य बिंदु है ।
तब, OL=LM=h2 और MB=10सेमी
आकृति द्वारा, यहाँ है, ΔOLB~ΔOMB
इसलिए OLOM=LDMB⇒(h2)2=LD10
⇒LD=5सेमी
यहाँ, CD शंकु को दो भागों में बांटता है ।
एक छोटे शंकु के लिए, त्रिज्या = 5 सेमी , ऊँचाई =h2
अब, आयतन =13π×5×5×h2=(25πh6)सेमी3
एक शंकु के छिन्नक के लिए, ऊपरी सिरे की त्रिज्या R=10 सेमी , निचले सिरे की त्रिज्या r=5 सेमी
ऊँचाई =h2 सेमी
आयतन =13×πh2⋅[(10)2+(5)2+10×5]=(175πh6)सेमी3
अब, अभीष्ट आयतनों का अनुपात =25πh6:175πh6=25:175=1:7
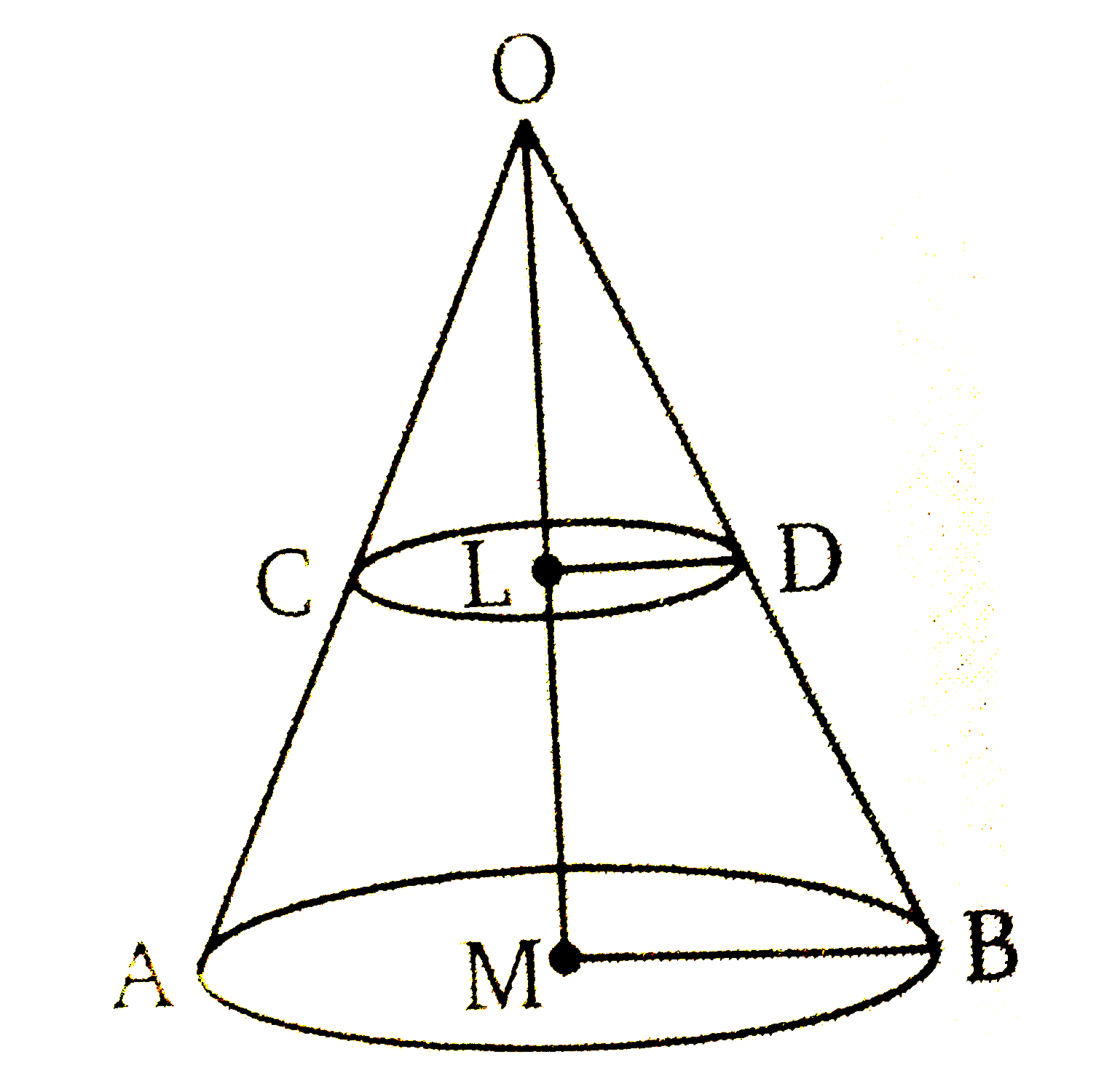
Topper's Solved these Questions
- पृष्ठीय क्षेत्रफल और आयतन BOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - विविध उदाहरण
10 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - BALAJI PUBLICATIONCHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - अभ्यास प्रश्न (13.1)
24 Videos
- निर्देशांक ज्यामिति BOOK - BALAJI PUBLICATIONCHAPTER - निर्देशांक ज्यामिति EXERCISE - स्वमूल्यांकन परिक्षण
26 Videos
- प्रश्न पत्र BOOK - BALAJI PUBLICATIONCHAPTER - प्रश्न पत्र EXERCISE - प्रश्न
89 Videos
Similar Questions
एक घन तथा इसके ऊपर लगे एक अर्द्धगोले से एक ठोस बना है । घन की प्रत्येक भुजा का मापन 5 सेमी तथा ऊपर लगे अर्द्धगोले का व्यास 4.2 सेमी है । रंगे भाग का कुल क्षेत्रफल ज्ञात कीजिए ।
View Solutionतीन घनों , जिनकी भुजाएँ क्रमशः 3 सेमी, 4 सेमी, 5 सेमी हैं, से एक घन बनायें तथा नये घन का पृष्ठीय क्षेत्रफल भी ज्ञात करें ।
View Solutionसिद्ध कीजिए की बिंदु (-4 ,-1 ) ,(-2 -4 ) ,(4 ,0 ) तथा (2 ,3 ) एक आयत के शीर्ष है|
View Solutionकिसी पूर्णांक m के लिए प्रत्येक धनात्मक सम पूर्णांक का रूप होगा -
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionएक 3.1 सेमी त्रिज्या में एक 2.3 सेमी की जीवा काटिए और उसके दोनों सिरों पर स्पर्श रेखाएं खींचिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionभूमिका |निर्देशांक तल #!#अंतरिक्ष में एक बिंदु के निर्देशांक#!#अष्टांश
View SolutionA right Pyramid has a square base with side of base 4 cm and the height of pyramid is 9cm. The pyramid is cut in three parts of equal heights by two planes parallel to its base. What is the ratio of the volume of the top, middle and the bottom part respectively?
एक सम पिरामिड का आधार 4 सेमी. भुजा वाला एक वर्ग है तथा पिसमिड की ऊँचाई 9 सेमी. है। पिरामिड को उसके आधार के' समांतर दो तलों द्वारा सामान ऊँचाई के तीन भागों में काटा गया है। क्रमशः ऊपरी, मध्य तथा निचले भागों के आयतन का अनुपात क्या हे?
View SolutionA right pyramid with square base has side of base 12cm. and height 40 cm. It is kept on its base. It is cut into 4 parts of equal heights by 3 cuts parallel to its base.What is the ratio of volume of the four parts? एक वर्ग आधार वाले पिरामिड के आधार की भुजा 12सेमी. तथा ऊँचाई 40 सेमी है। इसे इसके आधार पर रखा गया हे। इसे 3 कयवों से इसके आधार के समान्तर बराबर ऊँचाई वाले 4 भागों में काठा गया। चारों भागों के आयतन का अनुपात क्या हे?
View Solution
