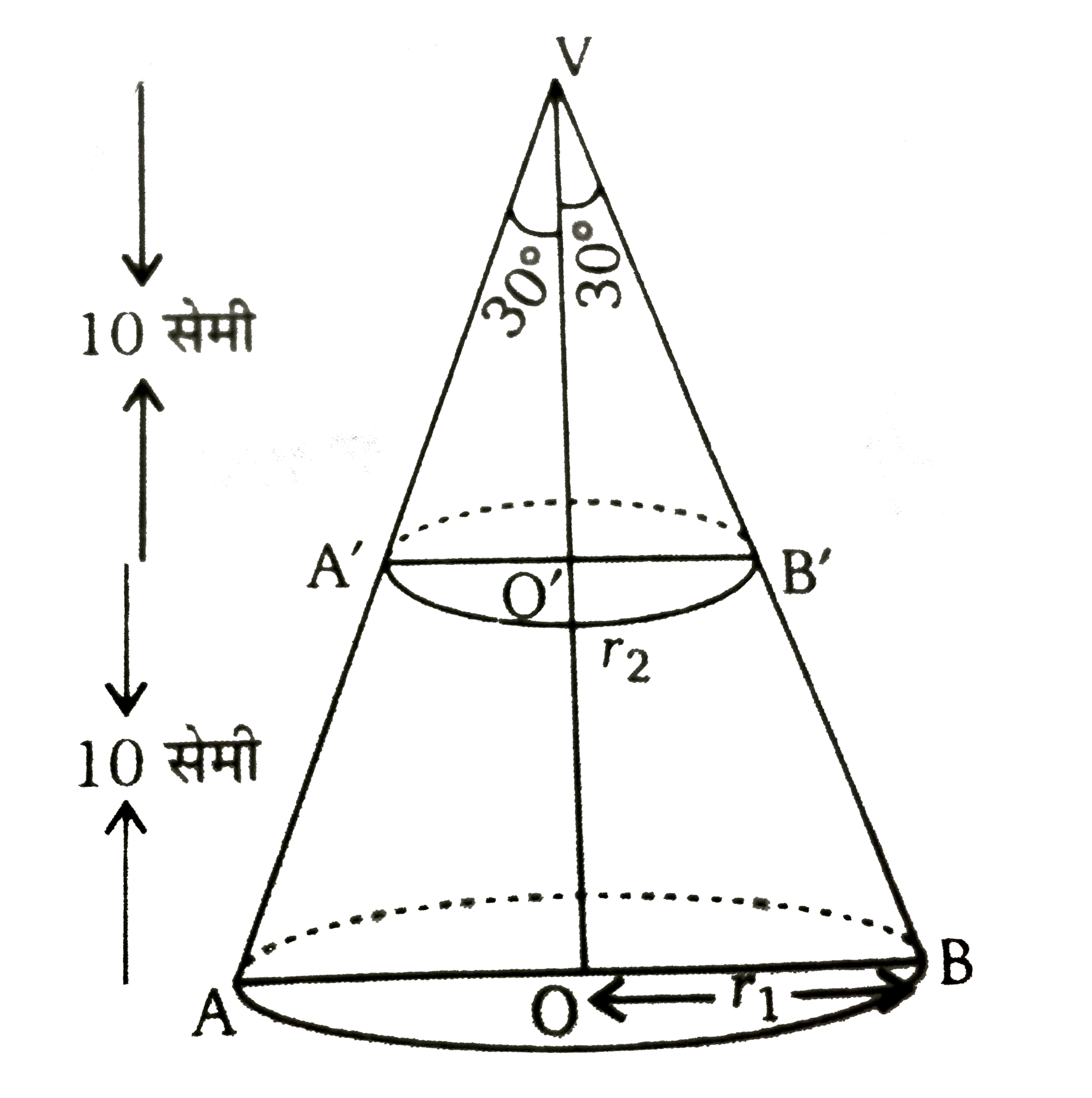
20 सेमी ऊँचाई और शीर्ष कोण 60 वाले एक लम्ब वृत्तीय शंकु को उसकी ऊँचाई के बेचों-बीच से होकर जाते हुए एक ताल से दो भागों में काटा गया है, जबकि तल, शंकु के आधार के समांतर है यदि इस प्राप्त शंकु के छिन्नक के व्यास $\frac{1}{16}$ सेमी वाले के एक तार के रूप में बदल दिया जाता है तो तार की लम्बाई ज्ञात कीजिए ।

Video Solution

Text Solution

Verified by Experts

${\tan 30}^{\circ} = \frac{O A}{V O}$ तथा ${\tan 30}^{\circ} = \frac{O' A'}{V O'}$
$\Rightarrow = \frac{1}{\sqrt{3}} = \frac{r_{1}}{20}$ तथा $\frac{1}{\sqrt{3}} = \frac{r_{2}}{10}$
$\Rightarrow r_{1} = \frac{20}{\sqrt{3}}$ सेमी तथा $r_{2} = \frac{10}{\sqrt{3}}$ सेमी
चूँकि छिन्नक का आयतन
$= \frac{1}{3} π (r_{1}^{2} + r_{2}^{2} + r_{1} r_{2}) h$
$= \frac{π}{3} (\frac{400}{3} + \frac{100}{3} + \frac{200}{3}) \times 10 = \frac{7000}{9} π {सेमी}^{3}$
माना कि $\frac{1}{16}$ सेमी व्यास वाले तार की लम्बाई $l$ है, तब
तार में प्रयुक्त धातु का आयतन $= π \times {(\frac{1}{32})}^{2} \times l = \frac{π l}{1024} {सेमी}^{3}$
इसलिए, तार में प्रयुक्त धातु का आयतन = छिन्नक का आयतन
$\Rightarrow \frac{π l}{1024} = \frac{7000 π}{9}$
$\Rightarrow l = \frac{7000 π}{9} \times \frac{1024}{π} = \frac{7000}{9} \times 1024 = 796444.4$ सेमी या 7964.4 मीटर

|

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-पृष्ठीय क्षेत्रफल और आयतन -स्वमूल्यांकन परीक्षण

Home
Ask Doubt
Profile