Question

लम्बवत्- अक्षों के प्रमेय की उपपत्ति करें [संकेतः (x, y) तल के लम्बवत् मूल बिन्दु से गुजरती अक्ष से किसी बिन्दु x-y की दूरी का वर्ग $(x^2+y^2)$ है।

Explanation

लम्बवत्-अक्षों की प्रमेय- किसी समतल पटल का उसके तल के लम्बवत् किसी अक्ष के परित: जड़त्व आघूर्ण उसके तल में स्थित दो परस्पर लम्बवत्-अक्षों (जिनके कटान बिन्दु से प्रथम अक्ष गुजरता है) के परितः जड़त्व आघूर्ण के योग के तुल्य होता है। समतल पटल के लिये इसे गणितीय रूप में इस प्रकार दिया जा सकता है--
उपपत्ति- `I_(Z)=I_(X)+I_(Y)`
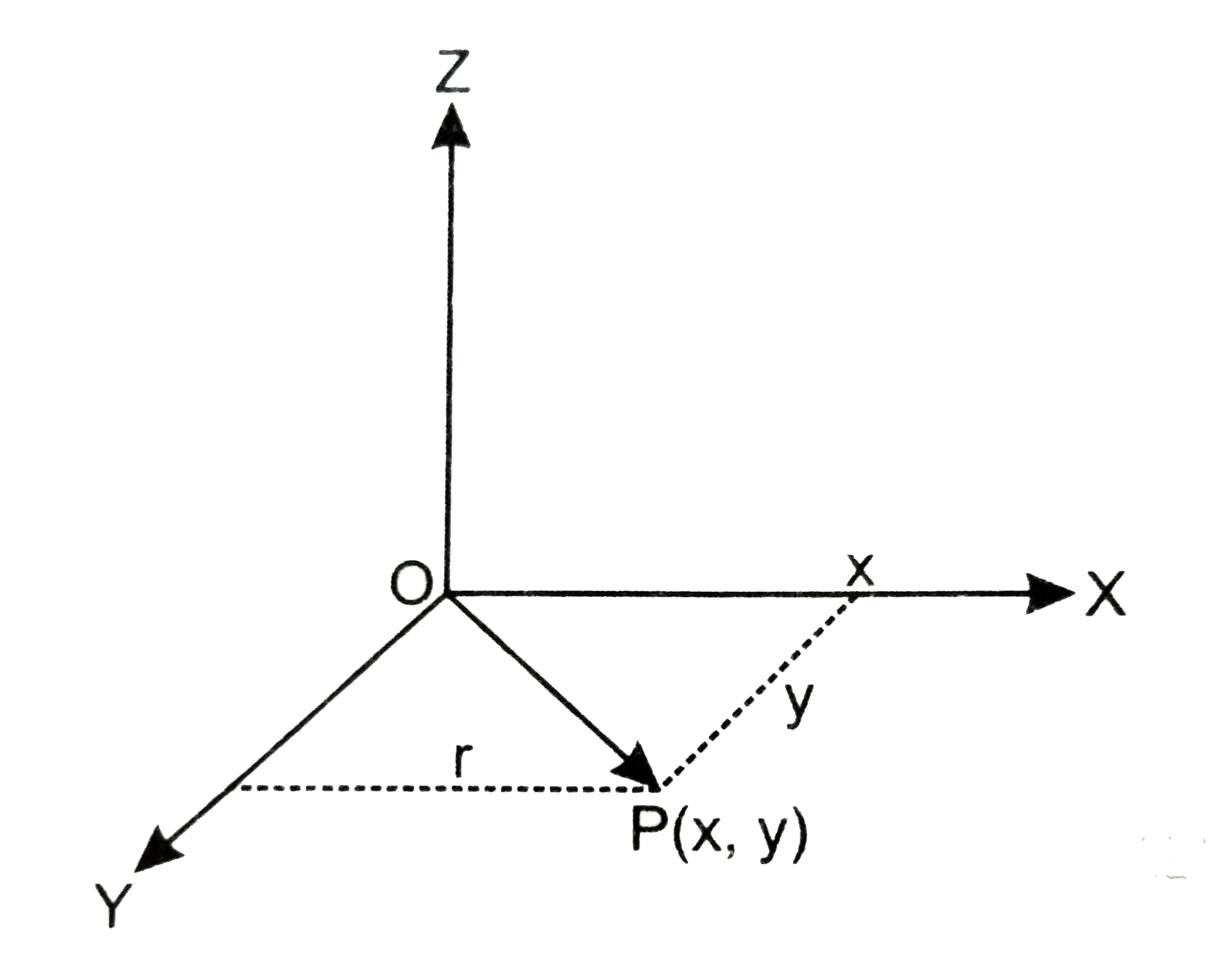
माना पटल अनेक कणों के द्वारा बना है जिसमें प्रत्येक कण का द्रव्यमान m है। माना m द्रव्यमान के कण P के निर्देशांक,x तथा y हैं तथा x-y तल से इसकी दूरी r है।
` therefore ` इस कण का अक्ष OZ के परितः जड़त्व आघूर्ण = ` mr ^ 2 `
यदि Z अक्ष के परितः सम्पूर्ण पटल का जड़त्व आघूर्ण ` I _ 2 ` है , तब
` I _ Z= sum m r ^ 2 = sum m ( x ^ 2 + y ^ 2 ) `
` = sum m x ^ 2 + sum my ^ 2 " " `...(ii)
अक्ष X तथा अक्ष Y के परितः सम्पूर्ण पटल का जड़त्व आघूर्ण ` I _ X ` तथा ` I _ Y ` है |
` therefore I _ X = sum my ^ 2 " " `...(iii)
` I _ Y = sum m x ^ 2 " " `...(iv)
` therefore ` समीकरण (ii ), (iii ) तथा (iv ) से, हम प्राप्त करते है |
` I _Z = I _ Y + I _ X = I _ X + I _ Y `