नीचे दिए गये समय के फलानो में कौन - (a ) सरल आवर्त गति (b ) आवर्ती परन्तु सरल आवर्त गति नहीं तथा (c ) अनावर्ती गति , का निरूपण करते है । प्रत्येक आवर्ती गति का आवर्तकाल गति , का निरूपण करता है । प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए । ( ω कोई धनात्मक अचार है ।)
(a) sinωt−cosωt
(b) sin3ωt
(c) 3cos(π4−2ωt)
(d) cosωt+cos3ωt+cos5ωt
(e) exp (−ω2t2)
(f) 1+ωt+ω2t2
(a) माना (x)t=sinωt−cosωt
=√2[1√2sinωt−1√2cosωt]
=√2[cos.π4sinωt−sin.π4cosωt]
=√2sin(ωt−π4)
स्पष्टतः उपरोक्त समीकरण निम्न रूप में है -
x=Asin(ωt±ϕ)
यह समीकरण SHM प्रदर्शित करता है ।
पुनः t=2πω का आवर्तकाल है ।
x(t+2πω)=√2sin[ω(t+2πω)−π4]
=√2(ωt+2π−π4)
=√2sin(ωt−π4)=x(t)
अतः आवर्तकाल T=2πω
तथा कला =−π4 या (2π−π4)
(b) माना x(t)=sin3t
अथवा x(t)=14(3sinωt−sinωt)
(∵sin3θ=3sinθ−4sin3θ)
उपरोक्त समीकरण दो सरल आवर्त गतियों का युग्म प्रदर्शित करती है । यह युग्म आवर्त है , किन्तु सरल आवर्त गति प्रकट नहीं करता ।
34sinωt का आवर्तकाल = 2πω=T
14sin3ωt का आवर्तकाल =2π3ω=T'=T3
अतः युग्म का आवर्तकाल
= न्यूनतम समय जिसके पश्चात युग्म समीकरण पुनरावृत्ति करता है ।
= LCM का T
तथा T3=T
(c) x(t)=3cos(π4−2ωt)
=3cos(2ωt−π4)
[∵cos(−θ)=cosθ]
उपरोक्त समीकरण निम्न रूप में है -
x(t)=Acos(ωt±ϕ)
अतः सरल आवर्त गति का आवर्तकाल
T=2π2ω=πω
(d) x(t)=cosωt+cos3ωt+cos5ωt
अतःcosωt, SHM प्रदर्शित करता है जिसका आवर्तकाल
=2πω=T ( माना )
cos3ωt, SHM प्रदर्शित करता है जिसका आवर्तकाल
=2π3ω=T5
cos5ωt , SHM प्रदर्शित करता है जिसका आवर्तकाल
=2π5ω=T5
न्यूनतम समय जिसमे गति फलन की पुनरावृत्ति होती है वह समय है । अतः दिया गया फलन आवर्ती फलन प्रकट करता है , किन्तु सरल आवर्त गति नहीं ।
(e ) x(t)=exp(−ω2t2)
दिया गया फलन चरघातांकी फलन है यह एकांक रूप से घटता है ।
x(t)→0 पर t→∞
इस मान की पुनरावृत्ति नहीं होतीहै । अतः यह अनावर्ती गति फलन प्रदर्शित करता है ।
(f) x(t)=1+ωt+ω2t2
यहाँ , t→∞
x(t)→∞
इस मान की पुनरावृत्ति नहीं होती है । अतः यह अनावर्ती फलन प्रदर्शित करता है ।
Topper's Solved these Questions
- BOOK - BALAJI PUBLICATIONCHAPTER - दोलन EXERCISE - अतिरिक्त अभ्यास6videos
दोलन
- BOOK - BALAJI PUBLICATIONCHAPTER - दोलन EXERCISE - बहुविकल्पीय प्रश्न36videos
दोलन
- BOOK - BALAJI PUBLICATIONCHAPTER - तरलों के यांत्रिक गुण (2):तरल गतिकी EXERCISE - पाठ्य -पुस्तक के प्रश्न44videos
तरलों के यांत्रिक गुण (2):तरल गतिकी
- BOOK - BALAJI PUBLICATIONCHAPTER - द्रव के तापीय गुणEXERCISE - पाठ्य-पुस्तक के प्रश्न22videos
द्रव के तापीय गुण
Similar Questions
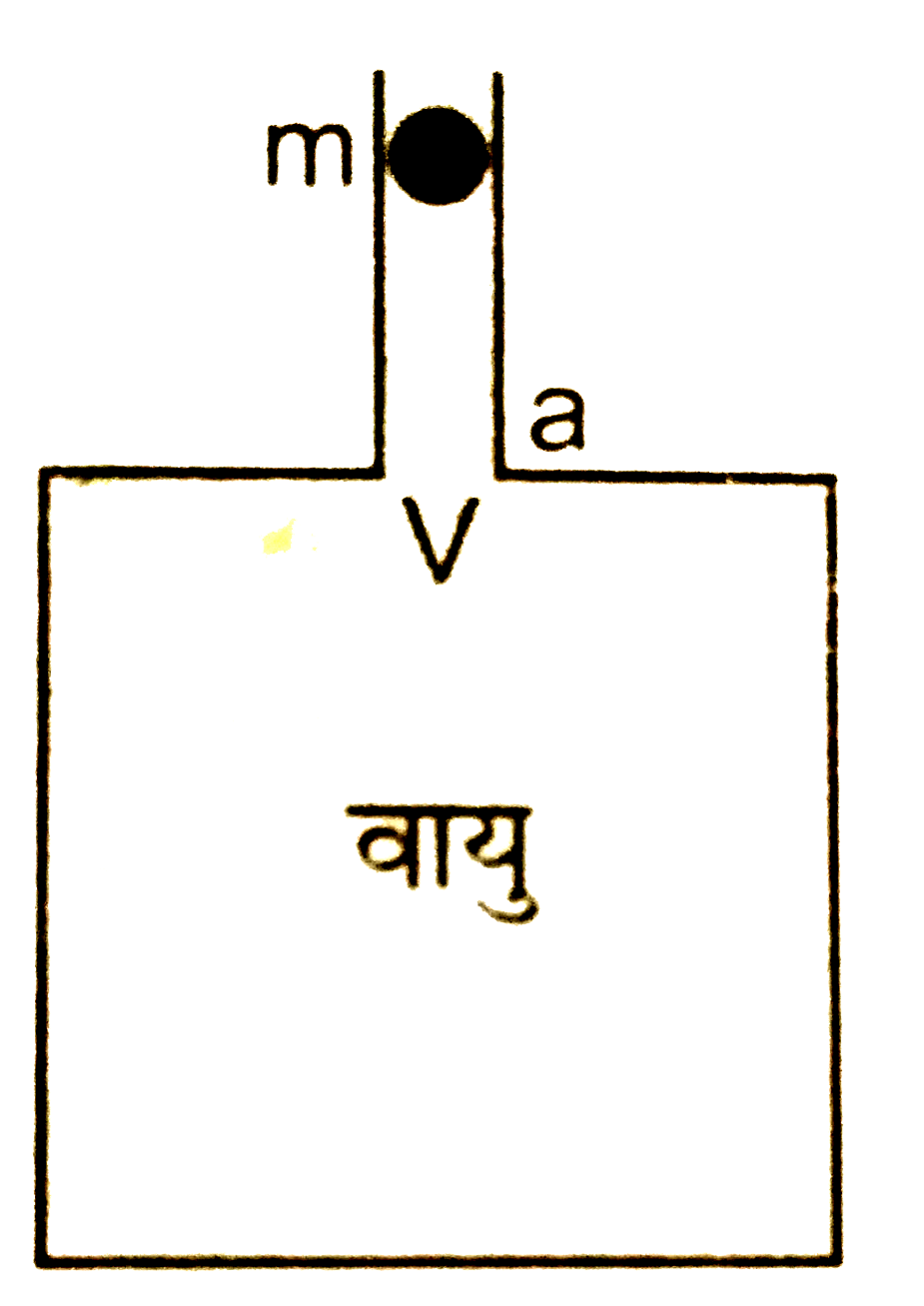
चित्र में दर्शाये अनुसार V आयतन के किसी वायु कक्ष कि ग्रीवा ( गर्दन) कि अनुप्रस्थ काट का क्षेत्रफल a है । इस ग्रीवा में m द्रव्यमान कि कोई गोली घर्षण के ऊपर - नीचे गति कार सकती है । यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते है , तो वह सरल आवर्त गति करती है । दाब - आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए ।
 42:28View Solution
42:28View Solutionकौन- सी गति सरल आवर्त गति है ?
48:14View Solutionमस्तिष्क की अपेक्षा मानव का पैरों पर रक्त चाप अधिक होता है ?
41:39View Solutionनिऑन तथा CO2 के त्रिक बिन्दु क्रमशः 24.57K तथा 216.55 K है। इस तापो को सेल्सियस तथा फॉरेनहाइट मापक्रमों में व्यक्त कीजिए।
43:08View Solutionगति का वर्णन | निर्देश तंत्र | सरल रेखीय गति | एकसमान गति
41:08View Solutionदोलन| सरल आवर्त गति का विस्थापन समीकरण
39:53View Solutionदोलन|सरल आवर्त गति #!# सरल आवर्त गति का वेग समीकरण
36:42View Solutionदोलन|सरल आवर्त गति #!#सरल आवर्त गति में त्वरण तथा आवर्तकाल का व्यंजक
50:17View Solutionदोलन|सरल आवर्त गति #!#सरल आवर्त गति में ऊर्जा
42:07View Solutionदोलन|सरल आवर्त गति #!#स्प्रिंगब्लॉक निकाय के सरल आवर्त गति
42:09View Solutionदोलन|सरल आवर्त गति #!#स्प्रिंग ब्लॉक निकाय की सरल आवर्त गति #!#आवर्तकाल
01:26:46View Solutionदोलन |सरल आवर्त गति #!#कोणीय सरल आवर्त गति #!#सरल लोलक
42:07View Solutionआवर्ती गति |दोलन गति या कंपन गति
45:25View Solutionएकसमान वृतीय गति और सरल आवर्त गति
01:21:20View Solutionसरल आवर्त गति|आवर्तकाल
01:22:02View Solutionगति का ग्राफीय निरूपण
01:19:24View Solution

