x -अक्ष पर चलते हुए एक कण का स्थान x=At3+Bt2+Ct+D के अनुसार बदलता है | SI इकाइयों में A, B, C एवं D के सांख्यिक मान क्रमशः 1,4,−2 तथा 5 है | (a) A, B, C तथा D के विमीय - सूत्र निकले | (b) समय t=4s पर कण का वेग निकालें | (c) t=4s पर कण का त्वरण निकालें | (d ) t=0 से t=4s के अंतराल में कण का औसत वेग निकाले | (e) t = 0 से t = 4s के अंतराल में कण का औसत त्वरण निकालें |
(a ) x,At3,Bt2,Ct एवं D की विमाएँ समान होगी | चूँकि इस समीकरण का एक पद x है , इसलिए इन पदों में से प्रत्येक की विमा लम्बाई की विमा के बराबर होगी | अतः,
[At3]=L या [A]=LT−3
[Bt2]=L या [B]=LT−2
[Ct]=L या [C]=LT−1
[D]=L
(b ) x=At3+Bt2+Ct+D
या v=dxdt=3At2+2Bt+C
अतः , t=4s पर कण का वेग,
v=[3×(1)×(4)2+2×(4)×(4)+(−2)]m/s
=(48+32−2)m/s=78m/s
चूँकि सभी जगह SI इकाइयों में संख्याएँ लिखी गयी है, अंतिम परिणाम भी SI इकाई में मिलेगी | इसलिए v का मान m/s में होगा |
अतः, v=78m/s
(c) v=3At2+2Bt+C
या a=dvdt=6At+2B
t=4s पर, a=[6×(1)×(4)+2×(4)]m/s2=32m/s2
(d ) x=At3+Bt2+Ct+D
t=0 पर , x=D=5m.
t=4s पर, x=[1×(4)3+4×(4)2+(−2)×(4)+5]m=125m
t = 0 से t = 4s तक में कण का विस्थापन = 125m−5m
=120m
अतः, इस अंतराल में कण का औसत वेग = 120m4s=30m/s
(e ) v=3At2+2Bt+C
t=0 पर, v1=C=−2m/s
t=4s पर, v2=[3×(1)×(4)2+2×(4)×(4)−2]m/s=78m/s
इस अंतराल में वेग में परिवर्तन
v2−v1=(78m/s)−(−2m/s)=80m/s
अतः, औसत त्वरण = 80m/s4s=20m/s2
Topper's Solved these Questions
- सरल रेखा में गति BOOK - HC VERMA HINDICHAPTER - सरल रेखा में गति EXERCISE - विचार हेतु प्रश्न
4 Videos
- सरल रेखा में गति BOOK - HC VERMA HINDICHAPTER - सरल रेखा में गति EXERCISE - सटीक उत्तरवाले प्रश्न (I)
6 Videos
- सरल रेखा में गति BOOK - HC VERMA HINDICHAPTER - सरल रेखा में गति EXERCISE - अभ्यास के प्रश्न
27 Videos
- सरल आवर्त गति पर आधारित अन्य गतियाँ BOOK - HC VERMA HINDICHAPTER - सरल आवर्त गति पर आधारित अन्य गतियाँ EXERCISE - अभ्यास के प्रश्न
8 Videos
- स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत BOOK - HC VERMA HINDICHAPTER - स्थितिज ऊर्जा एंव ऊर्जा - सरंक्षण का सिध्दांत EXERCISE - अभ्यास के प्रश्न
43 Videos
Similar Questions
यदि कोई कण एकसमान वेग से चल रहा हो,तो उसका औसत वेग , वेग तथा चाल सभी बराबर होंगे | इस कथन पर टिप्पणी करे |
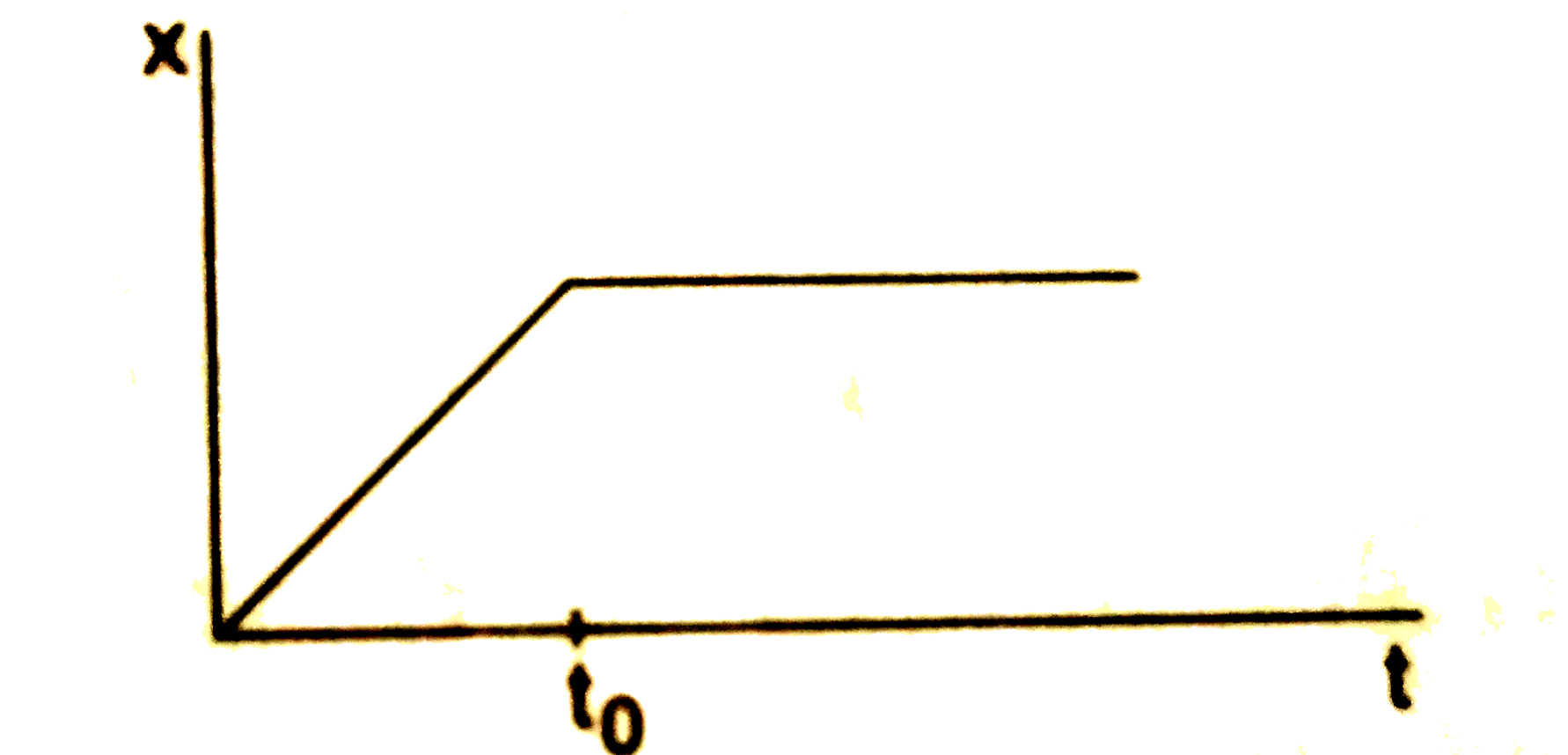
View Solutionचित्र में x - अक्ष पर चलते एक कण का विस्थापन - समय ग्राफ दिखाया गया है | इस ग्राफ से पता चलता है कि
View Solutionएक कण मूलबिंदु से प्रारम्भ कर x - अक्ष पर चलता हुआ x = 20 m पर पँहुचता है और फिर उसी रेखा पर वापस मुड़कर x = -20 m पर आ जाता है | इस पूरी अवधि में कण द्वारा तय की गई दुरी तथा उसका विस्थापन बताएँ |
View Solutionएक कण को एकसाथ दो आवर्त गतियाँ प्रदान की जाती है जिसकी दिशाएँ समान है तथा आवर्तकाल भी सामान हैं। एक का आयाम 3.0 cm तथा दूसरे का आयाम 4.0 cm है। परिणामी गति का आवर्तकाल निकालें यदि दोनों के बीच का कलांतर (a)0∘(b)60∘ तथा (c)90∘ हो।
View Solutionएक संयंत्र में 50 m ऊँचाई से गिरनेवाले जल का उपयोग विद्युत - ऊर्जा उत्पादन के लिए किया जाता हैं । यदि प्रतिघंटा 1.8×105 kg जल गिरता है तथा इसकी गुरुत्वीय स्थितिज ऊर्जा का आधा भाग विद्युत ऊर्जा में परिवर्तित किया जा सकता हैं , तो इससे 100 W के कितने बल्ब जलाए जा सकते हैं ?
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न का अनुकूलतम है निम्नलिखित शीर्ष पर है|
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionx-अक्ष एवं y-अक्ष के समांतर रेखाओं के समीकरण
View Solutionx-अक्ष के समान्तर समतल का समीकरण है
View SolutionA sum is divided among A, B, C and D such that the ratio of shares of A and B is 2:3, that of B and C is 1:2 and that of C and D is 3:4. If the difference between the shares of A and D is Rs. 648, then the sum of their shares is :
एक राशि A, B, C और D में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 2 : 3 है तथा B और C के हिस्सों का अनुपात 1: 2 है और C एवं D के हिस्सों का अनुपात 3 : 4 है| यदि A और D के हिस्सों में 648 रुपये का अंतर है, तो उनके हिस्सों का योग ज्ञात करें |
View SolutionA sum of Rs. 5200 is divided amongst A, B, C and D such that the ratio of shares of A and B is 2:3, that of B and C is 4:5 and that of C and D is 1:2. What is the difference between the shares of B and D?
5200 रुपये की राशि A, B, C और D में इस प्रकार विभाजित की जाती है कि A और B के हिस्सों का अनुपात 2: 3 है, B और C के हिस्सों का अनुपात 4 : 5 है तथा C और D के हिस्सों का अनुपात 1 : 2 है | B और D के हिस्सों में क्या अंतर है ?
View SolutionA certain sum is divided between A, B, C and D such that the ratio of the shares of A and B is 1 : 3, that of B and C is 2 : 5 and that of C and D is 2 : 3. If the difference between the shares of A and C is ₹3,510, then the share of D is :
एक राशि A, B, C और D के बीच विभाजित की जाती है, जैसे A और B के शेयरों का अनुपात 1: 3 है, B और C का अनुपात 2: 5 है और C और D का अनुपात 2 :3 है. यदि A और C के शेयरों के बीच अंतर ₹3,510 है, तो D का हिस्सा है
View Solutionरंगमंच पर पर्दे के पीछे का स्थान कहलाता है
View SolutionSix persons A, B, C, D, E and F are sitting in a line. E is between D and F. A is second to the right of F. C is at the extreme right. Who is sitting at second place to the left of C? छः व्यक्ति A, B, C, D, E और F एक पंक्ति में बैठे हुए हैं |E, D और F के बीच है| A, F के दायें को दूसरे स्थान पर है | C एकदम दायीं ओर है | C के बाएं को दूसरे स्थान पर कौन बैठा हुआ है ?
View Solution
