द्रव्यमान m वाले गुटके A को एक घर्षणरहित क्षैतिज टेबुल के बिंदु C से एक नगण्य भार वाली डोरी द्वारा जोड़कर रखा गया है | डोरी एक नगण्य भार वाली घर्षणरहित घिरनी B पर से जाती है जो डोरी के समानांतर दिशा में खींची जा सकती है |
(a) दिखाएँ की गुटके का त्वरण घिरनी के त्वरण का दोगुना होगा |
(b) घिरनी पर एक मनुष्य क्षैतिज दिशा में F बल लगा रहा है | गुटके का तथा घिरनी का त्वरण ज्ञात करें |
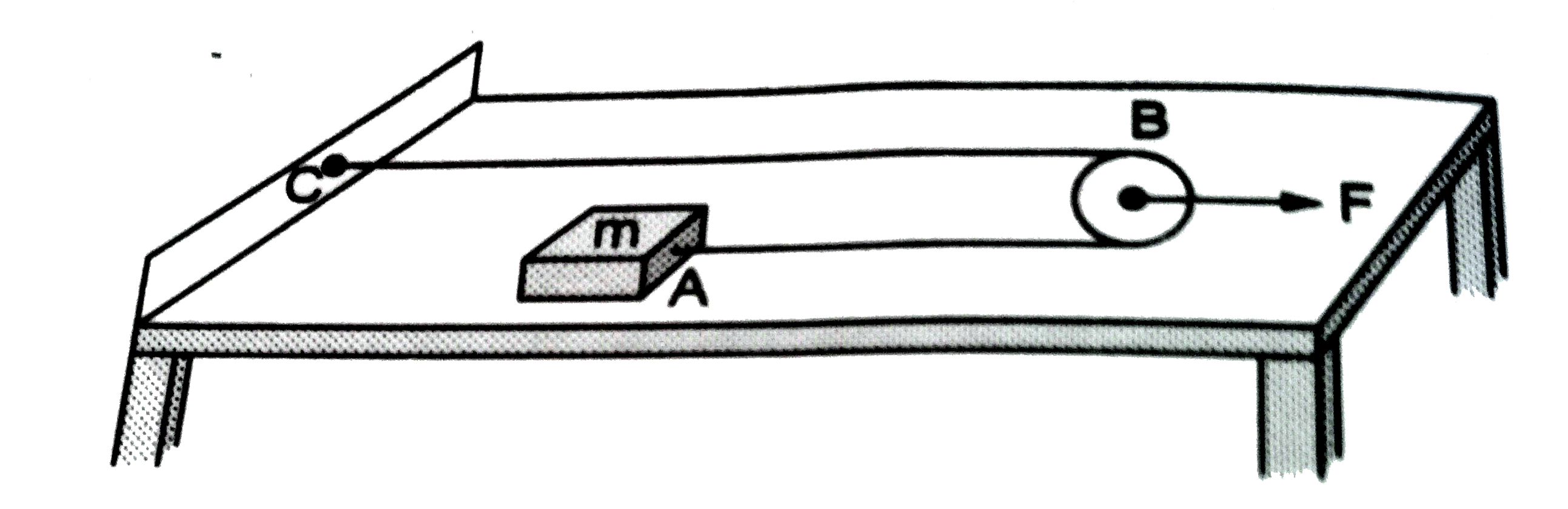
चित्र में टेबुल के किनारे से घिरनी तथा गुटके की दूरियाँ दिखाई गई हैं |

घिरनी का वेग तथा गुटके का वेग .
यदि घिरनी पर लिपटी डोरी की लंबाई हो और पूरी डोरी की लंबाई L हो, तो
.
यहाँ L तथा के मान निश्चित हैं | अब अवकलित करने पर,
या
किसी भी क्षण गुटके का वेग घिरनी के वेग से दोगुना होगा |
समीकरण (i) को पुन: अवकलित करने पर,
अत:, किसी भी क्षण गुटके का त्वरण घिरनी के त्वरण का दोगुना होगा |
(b) घिरनी को संहति मानें | इसपर क्षैतिज दिशा में लगते बल इस प्रकार हैं
(i) मनुष्य द्वारा F, दायीं ओर,
(ii) डोरी के BC भाग द्वारा T, बायीं ओर,
(iii) डोरी के BA भाग द्वारा T, बायीं ओर |
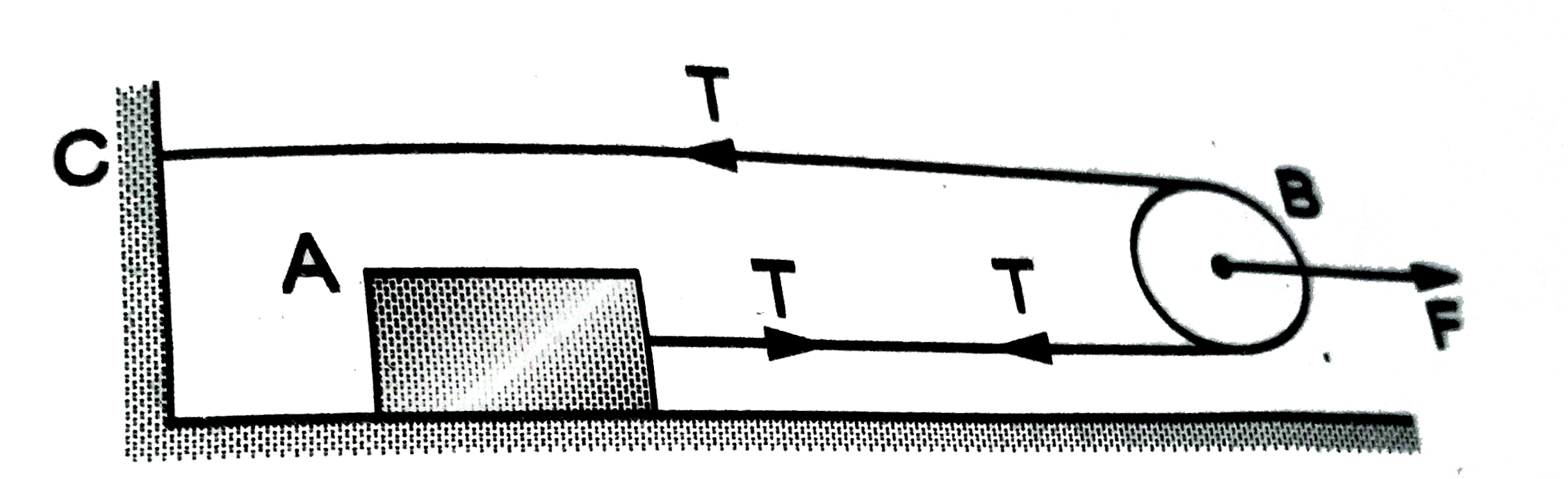
चूँकि घिरनी के द्रव्यमान को शून्य माना गया है, अत : न्यूटन के दूसरे गति-नियम से,
.
अब गुटके की गति पर विचार करें | इसपर एक ही क्षैतिज बल लग रहा है जो डोरी के BA भाग द्वारा दायीं ओर लगाया जा रहा है |
अत:, गुटके का त्वरण
तथा घिरनी का त्वरण .
Topper's Solved these Questions
- BOOK - HC VERMA HINDICHAPTER - न्यूटन के गति-नियम EXERCISE - अभ्यास 8.13videos
न्यूटन के गति-नियम
- BOOK - HC VERMA HINDICHAPTER - न्यूटन के गति-नियम EXERCISE - अभ्यास 8.23videos
न्यूटन के गति-नियम
- BOOK - HC VERMA HINDICHAPTER - ध्वनि तरंगो का अध्यारोपणEXERCISE - अभ्यास के प्रशन39videos
ध्वनि तरंगो का अध्यारोपण
- BOOK - HC VERMA HINDICHAPTER - प्रकाश का विवर्तन EXERCISE - अभ्यास के प्रश्न6videos
प्रकाश का विवर्तन
Similar Questions
चित्र में एक मनुष्य एक रस्सी के सहारे M द्रव्यमान के एक गुटके को निचे उतार रहा है । वह रस्सी इस तरह जाने देता है कि गुटके का त्वरण निचे की ओर a होता है ।
रस्सी के निचले सिरे पर उसमें तनाव निकालें ।04:43View Solutionएक घर्षणरहित घिरनी छत से एक क्लैम्प द्वारा टाँगकर रखी गई है । घिरनी से होकर जाती एक नगण्य भार वाली डोरी के सिरों से दो गुटके A तथा B, जिनके द्रव्यमान क्रमश : m1 तथा m2 हैं, बाँधकर लटकाए गए हैं ।
दोनों गुटकों के त्वरणों में संबंध बताएँ ।08:56View Solutionक्विंक की उपकरण में जब खिसकनेवाली नली को 2.50 cm खिसका दिया जाता है तो धवनि की त्रीवता अदिक्तम से न्यूनतम हो जाती है धवनि की आवर्ती निकले हवा में धवनि की चल =340 m/s
04:14View Solution5.0 cm चौड़ाई की एक लम्बी स्लिट पर माइक्रोवेव तरंगें लम्बवत पड़ रही हैं। यदि पहली अदीप्त फ्रिंज θ=30∘ पर बन रही हो, तो माइक्रोवेव का तरंगदैर्घ्य निकालें।
04:32View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
04:26View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
04:37View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
53:00View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
01:42View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
02:30View Solutionपरवलय x2=8y पर एक स्पर्श रेखा,जो X-अक्ष की धनात्मक दिशा के साथ कोण θ बनती है, का सभीकरण है
03:43View Solutionगुरुत्व त्वरण G के मान का परिकलन | द्रव्यमान तथा भार
03:25View Solutionएक तीन साल के बच्चे से किसी भी ऐसे विषय पर बातचीत की जा सकती है, जो उसके दायरे में आता हो।
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionआण्विक द्रव्यमान 390 वाले एक यौगिक को प्राप्त करने के लिए आण्विक द्रव्यमान 180 वाले एक यौगिक को CH_(3)COCl के साथ ऐसिलीकृत किया जाता है। पूर्व यौगिक के प्रति अणु पर उपस्थित ऐमीनो समूहों की संख्या है:
View Solution

